Gottfried Wilhelm Leibnitz, filozof i matematičar, u XVII. stoljeću je nezavisno od Newtona razvio osnove diferencijalnog računa rješavajući problem nalaženja tangente zadane krivulje u nekoj točki.
Neka je krivulja zadana s formulom ![]() , pri čemu je
, pri čemu je ![]() derivabilna funkcija. Sekanta
krivulje
derivabilna funkcija. Sekanta
krivulje ![]() koja prolazi
točkama
koja prolazi
točkama
![]() i
i ![]() , pri čemu je
, pri čemu je ![]() , je
pravac s koeficijentom (vidi sliku 5.2)
, je
pravac s koeficijentom (vidi sliku 5.2)
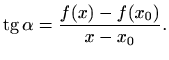
Kada ![]() , tada sekanta teži k tangenti krivulje
, tada sekanta teži k tangenti krivulje ![]() u
točki
u
točki
![]() , čiji je koeficijent smjera jednak
, čiji je koeficijent smjera jednak
![]() .
Također možete pogledati i
animaciju konvergencije
sekante prema tangenti.
Očito vrijedi
.
Također možete pogledati i
animaciju konvergencije
sekante prema tangenti.
Očito vrijedi
Stoga je jednadžba tangente na krivulju
Normala
na krivulju ![]() u točki
u točki
![]() je pravac koji prolazi kroz točku
je pravac koji prolazi kroz točku
![]() i okomit je na tangentu u toj točki.
Jednadžba normale stoga glasi
i okomit je na tangentu u toj točki.
Jednadžba normale stoga glasi
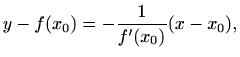
pri čemu smo pretpostavili da je