×   HOME PREDAVANJA

SADRŽAJ OSNOVE LINEARNA ALGEBRA VEKTORI I GEOMETRIJA FUNKCIJE DERIVACIJE NIZOVI I REDOVI INDEKS

VJEŽBE

SADRŽAJ OSNOVE LINEARNA ALGEBRA VEKTORI I GEOMETRIJA FUNKCIJE DERIVACIJE NIZOVI I REDOVI

KVIZ

SADRŽAJ OSNOVE LINEARNA ALGEBRA VEKTORI I GEOMETRIJA FUNKCIJE DERIVACIJE NIZOVI I REDOVI

PODSJETNIK

SADRŽAJ OSNOVE LINEARNA ALGEBRA VEKTORI I GEOMETRIJA FUNKCIJE DERIVACIJE NIZOVI I REDOVI

JAVA NETPLOT OCTAVE Traži ...

☰   matematika1 Monotonost     DERIVACIJE I PRIMJENE     Geometrijski ekstrem

Ekstremi

Kod ekstrema razlikujemo lokalne i globalne ekstreme. Za ispitivanje lokalnih ekstrema koristimo Fermatov teorem 5.6 i Teorem o monotonosti 5.11.

U definiciji lokalnih ekstrema te u iskazima i dokazima teorema o ekstremima, koristimo pojam $\varepsilon$ -okoline: $\varepsilon$ -okolina točke $x$ je interval $(x-\varepsilon , x+\varepsilon )$ pri čemu je $\varepsilon >0$ .

Definicija 5.4  

i)

Funkcija $f$ ima lokalni minimum $f(c)$ u točki $c\in \mathcal{D}$ ako postoji $\varepsilon$ -okolina točke $c$ takva da je $f$ neprekidna na toj okolini i pri tome vrijedi $f(x)>f(c)$ za svaki $x\in (c-\varepsilon ,c)\cup (c,c+\varepsilon )$ .

ii)

Funkcija $f$ ima lokalni maksimum $f(c)$ u točki $c\in \mathcal{D}$ ako postoji $\varepsilon$ -okolina točke $c$ takva da je $f$ neprekidna na toj okolini i pri tome vrijedi $f(x)<f(c)$ za svaki $x\in (c-\varepsilon ,c)\cup (c,c+\varepsilon )$ .

iii)

Funkcija $f$ ima globalni minimum $f(c)$ u točki $c\in \mathcal{D}$ ako je $f(x)\geq f(c)$ za svaki $x\in \mathcal{D}$ .

iv)

Funkcija $f$ ima globalni maksimum $f(c)$ u točki $c\in \mathcal{D}$ ako je $f(x)\leq f(c)$ za svaki $x\in \mathcal{D}$ .

Razlike između lokalnih i globalnih ekstrema prikazane su na slici 5.9. Kod lokalnih ekstrema se traži da je vrijednost funkcije u točki ekstrema strogo najmanja ili najveća na nekoj okolini. S druge strane, definicija globalnih ekstrema dozvoljava da se globalni ekstrem nalazi u više točaka pa čak i na nekom intervalu. Na primjer, za prikazanu funkciju $f:[a,j]:\to \mathbb{R}$ vrijedi sljedeće:

• ni jedna točka u intervalu $[a,b]$ nije ni lokalni, niti globalni ekstrem;
• u točki $c$ funkcija ima lokalni minimum, ali ne i globalni minimum;
• u točki $d$ funkcija ima lokalni maksimum, ali ne i globalni maksimum;
• sve točke u intervalu $[e,f]$ su točke globalnog minimuma, a ni jedna nije točka lokalnog minimuma;
• u točki $g$ funkcija istovremeno ima lokalni i globalni maksimum;
• u točki $i$ funkcija ima lokalni minimum.

Slika 5.9: Lokalni i globalni ekstremi

Za iskazivanje teorema koji daju uvjete za postojanje ekstrema, potrebna nam je sljedeća definicija.

Definicija 5.5   Neka je funkcija $f$ neprekidna u točki $c$ . Točka $c$ je stacionarna točka funkcije $f$ ako je $f'(c)=0$ . Točka $c$ je kritična točka funkcije $f$ ako je $c$ stacionarna točka ili ako $f$ nije derivabilna u točki $c$ .

Na primjer, za funkciju prikazanu na slici 5.9 stacionarne točke su sve točke u intervalima $(a,b)$ i $(e,f)$ te točke $c$ , $d$ i $g$ . Kritične točke su sve navedene točke te još točke $a$ , $b$ , $e$ , $f$ , $h$ i $i$ .

Razlikujemo dvije vrste uvjeta za postojanje lokalnog ekstrema u nekoj točki: nužan uvjet je uvjet kojeg ispunjava svaka točka u kojoj funkcija ima lokalni ekstrem; dovoljan uvjet je uvjet koji znači da funkcija u nekoj točki ima lokalni ekstrem čim je taj uvjet ispunjen.

Teorem 5.12   [Nužan uvjet za postojanje ekstrema] Neka je funkcija $f$ neprekidna u točki $c$ . Ako funkcija $f$ ima lokalni ekstrem u točki $c$ , tada je $c$ kritična točka funkcije $f$ .

Dokaz.

Ako funkcija $f$ nije derivabilna u točki $c$ , tada je teorem dokazan (nemamo što dokazivati). Ako je $f$ derivabilna u točki $c$ i ima lokalni ekstrem u toj točki, tada po definiciji 5.4 funkcija $f$ ima u točki $c$ najveću ili najmanju vijednost na nekoj $\varepsilon$ -okolini točke $c$ . Sada po Fermatovom teoremu 5.6 vrijedi $f'(c)=0$ .     

Q.E.D.

Na primjer, vidimo da su točke $c$ , $d$ , $g$ i $i$ u kojima funkcija prikazana na slici 5.9 ima lokalne ekstreme ujedno i kritične točke te funkcije. S druge strane, vidimo da teorem 5.12 daje samo nužan, a ne i dovoljan uvjet za postojanje lokalnog ekstrema, jer funkcija nema lokalne ekstreme u ostalim kritičnim točkama.

Teorem 5.12 ćemo ilustrirati još jednim primjerom.

Primjer 5.13  

a)

Funkcija $f(x)=x^2$ ima lokalni (i globalni) minimum u točki $x=0$ . Teorem 5.12 vrijedi jer je $f'(x)=2x$ pa je $f'(0)=0$ .

b)

Funkcija $f(x)=\vert x\vert$ ima lokalni (i globalni) minimum u točki $x=0$ . Teorem 5.12 vrijedi jer je funkcije nije derivabilna u točki 0 .

c)

Za funkciju $f(x)=x^3$ vrijedi $f'(x)=3x^2$ pa je $f'(0)=0$ . Međutim, $f(0)$ nije lokalni ekstrem pa vidimo da obrat teorema 5.12 ne vrijedi, odnosno teorem daje samo nužan uvjet za postojanje ekstrema.

Za iskazivanje teorema koji daju dovoljne uvjete za postojanje ekstrema, potrebna nam je sljedeća definicija.

Definicija 5.6   Funkcija $f$ mijenja predznak u točki $c$ , ako postoji $\varepsilon >0$ takav da su vrijednosti funkcije $f$ na intervalu $(c-\varepsilon ,c)$ stalnog i suprotnog predznaka od vrijednosti te funkcije na intervalu $(c,c+\varepsilon )$ .

Primijetimo da funkcija može mijenjati predznak u nekoj točki, a da pri tome nije definirana u toj točki.

Teorem 5.13   [Dovoljan uvjet za postojanje ekstrema] Ako prva derivacija $f'$ mijenja predznak u kritičnoj točki $c$ , tada funkcija $f$ ima lokalni ekstrem u točki $c$ . Pri tome vrijedi sljedeće: ako $f'$ mijenja predznak s $-$ na $+$ , tada je $f(c)$ lokalni minimum, a ako $f'$ mijenja predznak s $+$ na $-$ , tada je $f(c)$ lokalni maksimum.

Dokaz.

Ako derivacija $f'$ mijenja predznak s $-$ na $+$ , tada po teoremu 5.11 funkcija $f$ strogo pada na intervalu $(c-\varepsilon ,c)$ i strogo raste na intervalu $(c,c+\varepsilon )$ . Stoga funkcija $f$ ima u točki $c$ lokalni minimum po definiciji 5.4. Ako derivacija $f'$ mijenja predznak s $+$ na $-$ , tada na sličan način zaključujemo da funkcija $f$ ima u točki $c$ lokalni maksimum.     

Q.E.D.

Na primjer, funkcije iz primjera 5.13 a) i b) ispunjavaju uvjete teorema, dok funkcija iz primjera 5.13 c) te uvjete ne ispunjava.

Dovoljan uvjet za postojanje ekstrema možemo izraziti i pomoću druge derivacije.

Teorem 5.14   [Dovoljan uvjet za postojanje ekstrema] Neka je u stacionarnoj točki $c$ funkcija $f$ dva puta derivabilna. Ako je $f''(c)\neq 0$ , tada funkcija $f$ ima lokalni ekstrem u točki $c$ . Pri tome vrijedi sljedeće: ako je $f''(c)>0$ , tada je $f(c)$ lokalni minimum, a ako je $f''(c)<0$ , tada je $f(c)$ lokalni maksimum.

Dokaz.

Druga derivacija $f$ je derivacija prve derivacije pa pretpostavka da $f''(c)$ postoji zbog definicije 5.1 znači da prva derivacija $f'$ postoji ne samo u točki $c$ , već i u nekoj $\varepsilon$ -okolini točke $c$ . Neka je $f''(c)>0$ . Tada vrijedi

$$0<f''(c)=\lim_{x\to c}\frac{f'(x)-f'(c)}{x-c}= \lim_{x\to c}\frac{f'(x)}{x-c}.$$

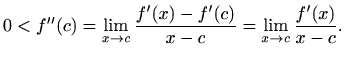
Zadnja jednakost vrijedi jer je $c$ stacionarna točka pa je $f'(c)=0$ . Za $x<c$ je $x-c<0$ pa gornja nejednakost povlači $f'(x)<0$ . Za $x>c$ je $x-c>0$ pa gornja nejednakost povlači $f'(x)>0$ . Dakle, prva derivacija $f'$ mijenja predznak u točki $c$ i to s $-$ na $+$ pa po teoremu 5.13 funkcija $f$ ima lokalni minimum u točki $c$ . Slično se dokaže da za $f'(c)=0$ i $f''(c)<0$ funkcija $f$ ima u točki $c$ lokalni maksimum.     

Q.E.D.

Prethodni dokaz možemo riječima iskazati i na sljedeći način: ako je $f''(c)>0$ , tada je $f''$ veća od nule i na nekoj okolini točke $c$ . To znači da je prva derivacija $f'$ strogo rastuća na toj okolini. Kako je $f'(c)=0$ , zaključujemo da je $f'$ negativna lijevo od točke $c$ i pozitivna desno do točke $c$ . To pak znači da funkcija $f$ strogo pada lijevo od točke $c$ , a strogo raste desno od točke $c$ pa je $c$ točka lokalnog minimuma.

Na primjer, funkcija $f(x)=x^2$ ispunjava uvjete teorema 5.14 u točki $x=0$ , jer je $f'(0)=0$ , a $f''(0)=2>0$ pa se u točki $x=0$ nalazi lokalni minimum. S druge strane, teorem ne možemo primijeniti na funkciju $f(x)=\vert x\vert$ u točki $x=0$ , jer nije derivabilna u toj točki. Teorem također ne možemo primijeniti niti na funkciju $f(x)=x^3$ u točki $x=0$ , jer je $f'(0)=0$ i $f''(0)=0$ . U tom slučaju možemo koristiti više derivacije (vidi teorem 5.18).

Poglavlja

• Geometrijski ekstrem

Monotonost     DERIVACIJE I PRIMJENE     Geometrijski ekstrem