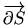 |
Stokesova formula je poopćenje Greenove formule iz poglavlja 2.5 na plohe i krivulje u prostoru.
Konzistentna orijentacija plohe i njenog ruba je kda orijentacija ruba zajedno s normalom u svakoj točki plohe čine desni koordinatni sustav. Možemo se izraziti i drukčije: plohu i njen rub orijentiramo tako da gledano iz vrha bilo koje normale rub bude pozitivno orijentiran. Konzistentne orijentacije plohe prikazane su na slici 3.12.
U skalarnom obliku Stokesova formula glasi
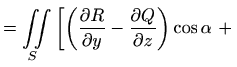 |
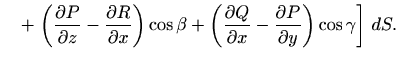 |
|
![$\displaystyle \quad + \left. \left(\displaystyle \frac{\partial P}{\partial z}-...
...x}- \displaystyle \frac{\partial P}{\partial y}\right)\cos\gamma \right] dS.$](img709.gif) |
duž ruba plohe
orijentiranog u negativnom smislu gledano iz vrha vektora
Ploha ![]() je gornja polusfera radijusa
je gornja polusfera radijusa ![]() . Iz slike 3.13
zaključujemo da je ploha
. Iz slike 3.13
zaključujemo da je ploha ![]() orijentirana vanjskom normalom sfere
orijentirana vanjskom normalom sfere
![]() te da je rub plohe kružnica
te da je rub plohe kružnica ![]() koja omeđuje krug
koja omeđuje krug ![]() .
.
Izračunajmo
![]() ,
,
![]() i
i
![]() (odnosno
(odnosno
![]() ) kako bi
primijenili skalarni oblik Stokesove formule. Vrijedi
) kako bi
primijenili skalarni oblik Stokesove formule. Vrijedi
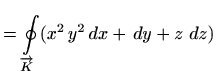
pa je
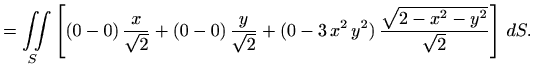 |
||
![$\displaystyle = \iint\limits_S \left[(0-0) \displaystyle \frac{x}{\sqrt{2}} +...
...-3 x^2 y^2) \displaystyle \frac{\sqrt{2-x^2-y^2}}{\sqrt{2}} \right] dS.$](img718.gif) |
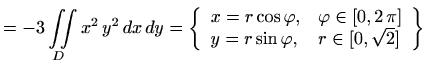 |
||
![$\displaystyle = -3\iint\limits_D x^2 y^2 dx dy= \left\{ \begin{array}{ll...
...\varphi \in[0,2 \pi] y=r\sin\varphi ,&r\in[0,\sqrt{2}] \end{array}\right\}$](img720.gif) |
||
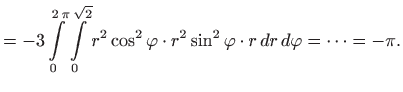 |