Natrag: PROBLEM NAJMANJIH KVADRATA   Gore: PROBLEM NAJMANJIH KVADRATA   Naprijed: Metoda najmanjih kvadrata  

Linearna regresija

Linearnu regresiju ćemo najbolje objasniti na primjeru. Neka je zadano pet točaka u ravnini

$$\begin{tabular}{r\vert lllll} x& 1 & 3 & 4 & 6 & 7 \hline y& 1 & 3 & 2 & 4 & 3 \end{tabular}$$

kao na slici 1.1.

Slika: Pet točaka u ravnini

Ukoliko bi pravac $y=kx+l$ prolazio kroz sve zadane točke, tada bi za svaku točku $(x_1,y_i)$, $i=1,2,\ldots, 5$ vrijedilo

$$k x_i+l=y_i.$$

U našem slučaju to daje sustav linearnih jednadžbi

$$k+l =1$$

$$3k+l =3$$

$$4k+l =2$$

$$6k+l =4$$

$$7k+l =3.$$

Ovo je sustav s pet jednadžbi i dvije nepoznanice $k$ i $l$. Matrični oblik sustava glasi

$$\begin{bmatrix}1 & 1 3 & 1 4 & 1 6 & 1 7 & 1 \end{bmatrix... ...atrix}k l \end{bmatrix}= \begin{bmatrix}1 3 2 4 3 \end{bmatrix},$$

odnosno $Ax=b$ gdje je

$$A=\begin{bmatrix}1 & 1 3 & 1 4 & 1 6 & 1 7 & 1 \end{bmatr... ...end{bmatrix}, \qquad b=y= \begin{bmatrix}1 3 2 4 3 \end{bmatrix}.$$

Ako bi ovaj sustav bio rješiv, tada bi vrijedilo $Ax-b=0$ odnosno $\Vert Ax-b\Vert=0$. Međutim, zadani sustav očito nije rješiv, pa se postavlja pitanje što možemo napraviti. Prirodan zahtjev je da izraz $Ax-b$ bude što bliži nul-stupcu, odnosno da norma $\Vert Ax-b\Vert$ bude što manja moguća. Taj zahtjev matematički zapisujemo kao

$$\Vert Ax-b\Vert \to \min.$$

Ako je $x$ rješenje ovog problema, tada je $x$ također i rješenje problema

$$\Vert Ax-b\Vert^2 \to \min$$

pa naziv problem najmanjih kvadrata slijedi iz definicije norme vektora.

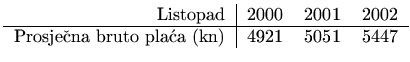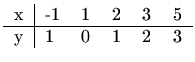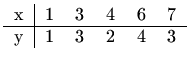
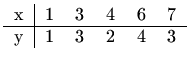
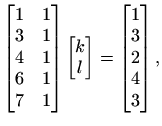
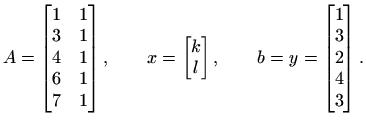
Postupak za rješavanje problema najmanjih kvadrata je u ovom slučaju jednostavan: rješenje $x$ dobit ćemo kao rješenje sustava od dvije jednadžbe i dvije nepoznanice

$$A^T A x=A^T b.$$

Kako je

$$A^TA=\begin{bmatrix}111 & 21 21 & 5 \end{bmatrix}, \qquad A^T b= \begin{bmatrix}63 13 \end{bmatrix},$$

rješenje $x$ dobijemo rješavanjem sustava

$$\begin{bmatrix}111 & 21 21 & 5 \end{bmatrix} \begin{bmatrix}k l \end{bmatrix} = \begin{bmatrix}63 13 \end{bmatrix}.$$

Ovaj sustav možemo lako rješiti Gaussovom eliminacijom ili, još jednostavnije, Cramerovim pravilom, pa je

$$k=\frac{\begin{vmatrix}63 & 21 13 & 5 \end{vmatrix}}{\begin{vm... ...nd{vmatrix}}{\begin{vmatrix}111 & 21 21 & 5 \end{vmatrix}}=\frac{120}{114}.$$

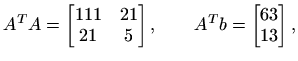
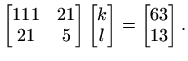
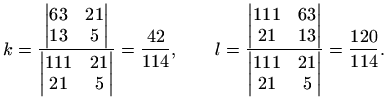
Geometrijska interpretacija rješenja je slijedeća (slika 1.2): pravac $y=kx+l$ "najbolje" prolazi točkama $(x_i,y_i)$, $i=1,2,\ldots, 5$ i smislu da je suma kvadrata udaljenosti između zadanih točaka $(x_i,y_i)$ i točaka na pravcu $(x_i,kx_i+l)$ minimalna. Drugim riječima,

$$\sum_{i=1}^5 [y_i - (kx_i+l)]^2 \to \min.$$

Slika: Rješenje problema najmanjih kvadrata

Napomena 1.1   Ravninski problem najmanjih kvadrata zove se linearna regresija, a pravac $y=kx+l$ zove se regresijski pravac.

Rješenje prethodnog problem i slike 1.1 i 1.2 mogu se dobiti pomoću slijedećeg Matlab (Octave) programa

Octave On-line

x=[1 3 4 6 7] y=[1 3 2 4 3] plot(x,y,'b*') A=[x' ones(5,1)] b=y' xLS=(A'*A)\(A'*b) k=xLS(1) l=xLS(2) yLS=k*x+l plot(x,y,'b*',x,yLS,'r')

     

  

[Octave On-line Home]    [Octave User's Guide]

U Matlabovoj sintaksi A' je transponirana matrica matrice $A$, ones(5,1) je vektor dimenzije $5\times 1$ sa svim elementima jednakim $1$, dok izraz oblika x=A\b daje rješenje sustava $Ax=b$. Štoviše, u slučaju preodređenog sustava kao u našem primjeru, Matlabova naredba xLS=A\b će automatski dati rješenje problema najmanjih kvadrata. Zamijenite liniju xLS=(A'*A)\(A'*b) s xLS=A\b i uvjerite se da su rješenja ista!

Zadatak 1.1   Prema podacima Državnog zavoda za statistiku (http://www.dzs.hr) prosječna bruto plaća u listopadu kroz protekle tri godine bila je slijedeća

$$\begin{tabular}{r\vert lll} Listopad & 2000 & 2001 & 2002 \hline Prosječna bruto plaća (kn)& 4921 & 5051 & 5447 \end{tabular}$$

Izračunajte i nacrtajte regresijski pravac i predvidite kolika će biti bruto plaća u listopadu 2003. Rješenje provjerite pomoću Matlaba ili programa Octave On-line.

Zadatak 1.2   Kroz točke

$$\begin{tabular}{r\vert lllll} x & -1 & 1 & 2 & 3 & 5 \hline y & 1 & 0 & 1 & 2 & 3 \end{tabular}$$

provucite najbolji pravac u smislu najmanjih kvadrata. Nacrtajte zadane točke i dobiveni pravac te provjerite rješenje pomoću Matlaba ili programa Octave On-line.

Natrag: PROBLEM NAJMANJIH KVADRATA   Gore: PROBLEM NAJMANJIH KVADRATA   Naprijed: Metoda najmanjih kvadrata