Natrag: Linearna regresija   Gore: PROBLEM NAJMANJIH KVADRATA   Naprijed: QR RASTAV  

Metoda najmanjih kvadrata

Postupak iz prethodnog poglavlja primjenjiv je i na višedimenzionalne probleme. U ovom poglavlju pokazat ćemo da je postupak primjenjiv uvijek kada matrica sustava $A$ ima linearno nezavisne stupce te je u tom slučaju rješenje problema najmanjih kvadrata jedinstveno.

Neka je zadan preodređeni sustav $Ax=b$ od $m$ jednadžbi s $n$ nepoznanica, pri čemu je $m>n$. Kako za normu vektora $x$ vrijedi $\Vert x\Vert^2=x^Tx$, problem najmanjih kvadrata

$$% \begin{equation}\label{ls1} \Vert Ax-b\Vert^2\to \min$$

možemo zapisati kao

$$% \begin{equation}\label{ls2} (Ax-b)^T(Ax-b) \to \min.$$

Uvedimo oznaku

$$Q(x) =\Vert Ax-b\Vert^2=(Ax-b)^T(Ax-b)$$

$$=x^TA^TAx-b^tAx-x^tA^tb+b^Tb$$ (1.1)

$$=x^TBx-2x^Tc+\beta$$

gdje je

$$B=A^TA,\qquad c=A^Tb,\qquad \beta=\Vert b\Vert^2.$$

Ideju za postupak rješavanja daje nam jednodimenzionalni slučaj: ako su $x$, $B$, $c$ i $\beta$ realni brojevi, tada je $Q(x)=Bx^2-2xc+\beta$ kvadratna parabola čiji se minimum nalazi u točki

$$x=\frac{c}{B}.$$

U višedimenzionalnom slučaju tome odgovara

$$x=B^{-1}c$$

pa je $x$ rješenje sustava

$$Bx=c,$$

odnosno

$$A^T A x=A^T b.$$

Ova jednadžba zove se normalna jednadžba. Dokažimo sada da ovaj intuitivni postupak zaista daje rješenje.

Teorem 1.1   Neka su stupci matrice $A$ linearno nezavisni, odnosno $\mathop{\mathrm{rang}}\nolimits (A)=n$. Tada je rješenje $x$ problema najmanjih kvadrata $Q(x)\to \min$ ujedno i jedinstveno rješenje normalne jednadžbe $A^TAx=A^Tb$.

Dokaz.

Neka je $y$ bilo koji $n$-dimenzionalni vektor i neka je $h=y-x$. Tada je prema (1.1)

$$Q(y) =y^TBy-2y^Tc+\beta$$

$$=(x+h)^TB(x+h)-2(x+h)^Tc+\beta$$

$$=x^TBx+h^TBx+x^TBh+h^TBh -2x^Tc-2h^Tc+\beta.$$

Kako je $Bx=c$, to je

$$h^TBx=h^Tc,$$

a kako se radi o matricama dimenzije $1$, to je zbog $B ^T=(A^TA)^T=B$ i

$$x^TBh=(x^TBh)^T= h^T B^T x=h^TBx=h^Tc.$$

Uvrštavanje u $Q(y)$ daje

$$Q(y)=x^TBx+h^TBh-2x^Tc+\beta=Q(x)+h^TBh.$$

Izraz $h^TBh$ je veći ili jednak od nule:

$$h^TBh=h^TA^TAh=(Ah)^TAh=\Vert Ah\Vert^2.$$

Dakle, uvijek je

$$Q(y)\geq Q(x),$$

odnosno vrijednost $Q(x)$ je zaista najmanja moguća.

Dokažimo sada da je rješenje $x$ jedinstveno. Ako je

$$Q(y)=Q(x),\qquad x\neq y,$$

tada je $\Vert Ah\Vert=0$. No, tada je i $Ah=0$ (samo nul-vektor ima normu jednaku nula), što zajedno s $h=y-x\neq 0$ znači da su stupci matrice $A$ linearno zavisni. To je kontradikcija pa je teorem dokazan.

Q.E.D.

Primjetimo da su vektori $Ax$ i $Ax-b$ međusobno okomiti:

$$(Ax)\cdot (Ax-b)=(Ax)^T(Ax-b)=x^T A^T(Ax-b)=0.$$

Geometrijski to znači da je vektor $Ax$ ortogonalna projekcija vektora $b$ na skup $\{Ay: y \textrm{ proizvoljan}\}$. Nadalje, vektori $Ax$, $b$ i $Ax-b$ tvore pravokutni trokut s hipotenuzom $b$.

Rješenje problema najmanjih kvadrata $x$ zove se još i kvadratična prilagodba sustavu $Ax=b$ u smislu najmanjih kvadrata. Kvalitetu prilagodbe mjerimo s

$$q=\sqrt{\frac{Q(x)}{(Q(0)}}=\frac{\Vert Ax-b\Vert}{\Vert b\Vert }.$$

Iz činjenice da je $b$ hipotenuza pravokutnog trokuta sa stranicama $Ax$, $Ax-b$ i $b$ slijedi da je $q$ uvijek je između 0 i 1. Ukoliko je $q=0$ tada je prilagodba najbolja moguća, odnosno $x$ je točno rješenje suatava $Ax=b$. Ukoliko je $q$ mali, prilagodba je dobra, a ukoliko je $q$ blizu jedan, prilagodba je loša.

Primjer 1.1   Riješimo sustav

$$x+y =0$$

$$y+z =1$$

$$x+z =0$$

$$-x+y+z =1$$

$$-x-z =0$$

u smislu najmanjih kvadrata. U matričnom obliku sustav glasi

$$\begin{bmatrix}1& 1 &0\\ 0 & 1 & 1\\ 1 & 0 & 1\\ -1 & 1 & 1 ... ...matrix}x y z \end{bmatrix}=\begin{bmatrix}0 1 0 1 0 \end{bmatrix}.$$

Normalna jednadžba glasi

$$\begin{bmatrix} 4 & 0 & 1\\ 0 & 3 & 2\\ 1 & 2 & 4 \end{bmatrix}\begin{bmatrix}x y z \end{bmatrix}=\begin{bmatrix}-1 2 2 \end{bmatrix}$$

pa je rješenje dano s

$$x=-\frac{10}{29},\qquad y=\frac{12}{29}, \qquad z=\frac{11}{29}.$$

Kvaliteta prilagodbe je

$$q=0.1857$$

Odgovarajući Matlab program glasi

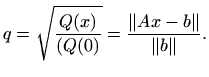
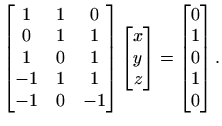
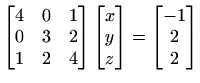
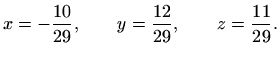
Octave On-line

A = [1 1 0; 0 1 1; 1 0 1; -1 1 1; -1 0 -1] b=[0 1 0 1 0]' B=A'*A c=A'*b x=B\c % ili krace x=A\b q=norm(A*x-b)/norm(b)

     

  

[Octave On-line Home]    [Octave User's Guide]

Primjer 1.2   Kroz točke

$$\begin{tabular}{r\vert lllll} x& 1 & 2 & 4 & 5 & 6 \hline y& 0 & 1 & 4 & 8 & 14 \end{tabular}$$

provucimo kvadratnu parabolu

$$y=ax^2+bx+c$$

koja ima najbolju kvadratičnu prilagodbu. Dakle, moramo naći koeficijente parabole tako da je

$$\sum_{i=1}^5 (y_i-axi^2-bx_i-c)^2 \to \min.$$

Ovaj problem možemo zapisati kao problem najmanjih kvadrata

$$\begin{bmatrix}1 & 1 & 1 \\ 4 & 2 & 1 16 & 4 & 1 25 & 5 & 1\... ...x}a b c \end{bmatrix}=\begin{bmatrix}0 1 4 8 14 \end{bmatrix}.$$

Rješavanje normalne jednadžbe daje

$$\begin{bmatrix}a b c \end{bmatrix} \approx \begin{bmatrix} 0.68994\\ -2.16071\\ 1.86364 \end{bmatrix},$$

a kvaliteta prilagodbe iznosi $q=0.0562$. Zadane točke i dobivena parabola prikazane su na slici 1.3.

Slika 1.3: Parabola s najboljom prilagodbom

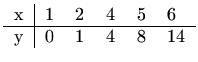
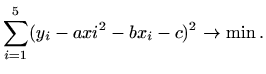
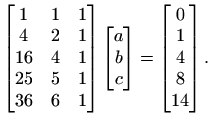
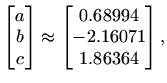
Parabola i slike mogu se dobiti slijedećim Matlab programom

Octave On-line

A = [1 1 1 4 2 1 16 4 1 25 5 1 36 6 1] y = [0 1 4 8 14]' % rjesenje xLS=A\y % kvaliteta prilagodbe q=norm(A*xLS-y)/norm(y) % slike x=[1 2 4 5 6]' plot(x,y,'r*') hold % gusca mreza radi bolje slike parabole x1=1:0.1:6 y1=xLS(1)*x1.^2+xLS(2)*x1+xLS(3) plot(x1,y1,'b')

     

  

[Octave On-line Home]    [Octave User's Guide]

Napomena 1.2   Vidimo da je puni stupčani rang matrice $A$ nužan za funkcioniranje metode normalnih jednadžbi jer bi u protivnom matrica $B=A^TA$ bila singularna. Ukoliko matrica $A$ nema puni stupčani rang tada rješenje problema najmanjih kvadrata nije jedinstveno i za rješavanje problema ne može se koristiti normalna jednadžbe. U tom slučaju od svih mogućih (beskonačno) rješenja, zanima nas ono koje samo po sebi ima najmanju normu. Za rješavanje takvih problema koristimo ili QR rastav s pivotiranjem po stupcima ili rastav singularnih vrijednosti (SVD ili singular value decomposition). Nadalje, ove dvije metode je zbog njihovih svojstava (numeričke stabilnosti) poželjno koristiti i kada su stupci matrice $A$ gotovo linearno zavisni. Detaljna analiza ovih slučajeva izlazi izvan okvira kolegija, pa je izostavljamo.

Natrag: Linearna regresija   Gore: PROBLEM NAJMANJIH KVADRATA   Naprijed: QR RASTAV