
Next: The Effects of Dispersal
Up: Modeling the Population Dynamics
Previous: Modeling the Population Dynamics
An individual lesion on a leaf grows at a measurable and well-defined radial
growth rate,  , per day, and after a certain latency period (
, per day, and after a certain latency period (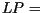 five days for P. infestans) the invaded area of the leaf sporulates for
a certain number of days (
five days for P. infestans) the invaded area of the leaf sporulates for
a certain number of days (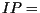 1 day). The progress of an individual late
blight lesion on a single leaf is depicted in Figure 1. During
the infectious period spores are released at a given rate,
1 day). The progress of an individual late
blight lesion on a single leaf is depicted in Figure 1. During
the infectious period spores are released at a given rate,  , per area per
day, and these spores disperse. Some fraction of spores which settle from the
air are intercepted by leaves (with probability
, per area per
day, and these spores disperse. Some fraction of spores which settle from the
air are intercepted by leaves (with probability
 ), and of these
intercepted spores a fraction,
), and of these
intercepted spores a fraction,
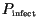 , successfully germinates and infects
the plant (provided it does not land on area already occupied by a lesion).
The parameters of the model and nominal values are listed in Table
1.
, successfully germinates and infects
the plant (provided it does not land on area already occupied by a lesion).
The parameters of the model and nominal values are listed in Table
1.
When a lesion is 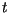 days old, the area that it adds is the difference
between the area it is,
days old, the area that it adds is the difference
between the area it is,
 and the area it will
become on the next day,
and the area it will
become on the next day,
 . Thus,
. Thus,
Consequently, when a lesion is six or more days old, the area which is
sporulating is the area which was added to the lesion 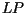 days ago. Since
days ago. Since
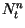 is the density of lesions of age
is the density of lesions of age  days on day
days on day  ,
the number of spores produced by these lesions is
,
the number of spores produced by these lesions is
This is an idealization based on the assumption that leaves of the plant are
much larger than the lesions; stability of our results to relaxation of this
assumption will be investigated in later sections.
Assuming that all dispersal happens locally, the number of spores arriving is
the number of spores produced and a model for reproduction of
lesions can be written
The combination of probabilities in the first line is the
probability of the composite event that (first) a spore lands on a leaf and
is not subsequently knocked off (
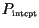 ), that (second) the spore is able to
germinate and penetrate the outer skin of the leaf (
), that (second) the spore is able to
germinate and penetrate the outer skin of the leaf (
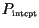 ), and that (third)
the spore has landed on leaf area not currently occupied by a lesion (
), and that (third)
the spore has landed on leaf area not currently occupied by a lesion (
 ).
Probabilistic parameters are set using the `rule of thumb' that 1 parent
lesion produces a net 10 daughter lesions in the Netherlands in ideal
circumstances [23]. The probability of a spore landing on unoccupied leaf area can be calculated from the ratio of the total leaf
area and the total area occupied by lesions,
).
Probabilistic parameters are set using the `rule of thumb' that 1 parent
lesion produces a net 10 daughter lesions in the Netherlands in ideal
circumstances [23]. The probability of a spore landing on unoccupied leaf area can be calculated from the ratio of the total leaf
area and the total area occupied by lesions,
![\begin{displaymath}
P_{\mbox{\tiny unocc}}(N_1^n, N_2^n, \cdots ) = \max\left[\f...
...pi \Delta r^2}{LAI} \sum_{t=1}^\infty
N_t^n \ t^2 , 0\right].
\end{displaymath}](img48.gif) |
(1) |
The number of spores produced the previous day is given by


Next: The Effects of Dispersal
Up: Modeling the Population Dynamics
Previous: Modeling the Population Dynamics
James Powell, Ivan Slapnicar and Wopke van der Werf
2002-06-01
![]() , per day, and after a certain latency period (
, per day, and after a certain latency period (![]() five days for P. infestans) the invaded area of the leaf sporulates for
a certain number of days (
five days for P. infestans) the invaded area of the leaf sporulates for
a certain number of days (![]() 1 day). The progress of an individual late
blight lesion on a single leaf is depicted in Figure 1. During
the infectious period spores are released at a given rate,
1 day). The progress of an individual late
blight lesion on a single leaf is depicted in Figure 1. During
the infectious period spores are released at a given rate, ![]() , per area per
day, and these spores disperse. Some fraction of spores which settle from the
air are intercepted by leaves (with probability
, per area per
day, and these spores disperse. Some fraction of spores which settle from the
air are intercepted by leaves (with probability
![]() ), and of these
intercepted spores a fraction,
), and of these
intercepted spores a fraction,
![]() , successfully germinates and infects
the plant (provided it does not land on area already occupied by a lesion).
The parameters of the model and nominal values are listed in Table
1.
, successfully germinates and infects
the plant (provided it does not land on area already occupied by a lesion).
The parameters of the model and nominal values are listed in Table
1.
![]() days old, the area that it adds is the difference
between the area it is,
days old, the area that it adds is the difference
between the area it is,
![]() and the area it will
become on the next day,
and the area it will
become on the next day,
![]() . Thus,
. Thus,