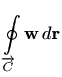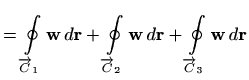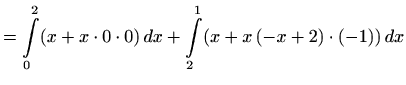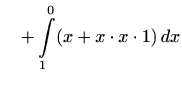Primjer 2.5 Izračunajmo cirkulaciju ravninskog vektorskog polja
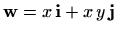
po
- a)
- središnjoj kružnici radijusa
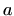 priozvoljne orjentacije,
priozvoljne orjentacije,
- b)
- rubu trokuta
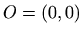 ,
, 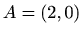 ,
, 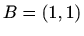 orjentiranom u pozitivnom smislu.
orjentiranom u pozitivnom smislu.
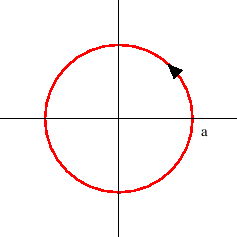
Kružnica iz točke a) prikazana je na slici 2.6.
Slika 2.6:
Pozitivno orijentirana kružnica
 |
Jedna parametrizacija kružnice glasi
pa vrijedi
Za kružnicu orjentiranu u negativnom smislu zbog promjene orijentacije
vrijedi
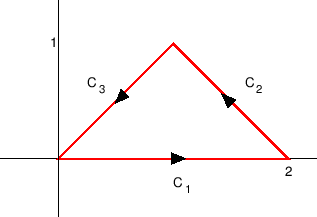
Trokut iz točke b) prikazan je na slici 2.7.
Slika 2.7:
Pozitivno orijentirani trokut
 |
Glatke dijelove krivulje
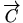 parametriziramo na sljedeći način:
parametriziramo na sljedeći način:
Vrijedi
![$\displaystyle \overrightarrow{C}\ \ldots \ \left\{\begin{array}{l} x=a\cos t, \\ y=a\sin t,
\end{array}\right. \qquad t\in[0,2\,\pi]
$](img420.gif)
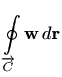
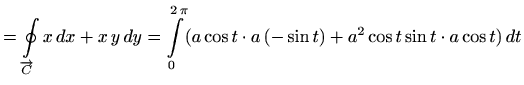
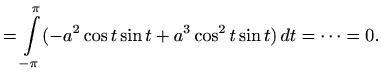
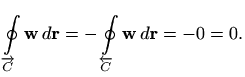
![]() parametriziramo na sljedeći način:
parametriziramo na sljedeći način: