krivuljni integral vektorskog polja postaje integral totalnog diferencijala, odnosno vrijedi
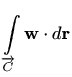 |
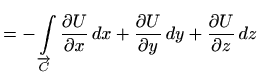 |
|
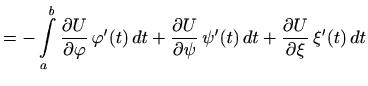 |
||
![$\displaystyle =\int\limits_b^a d\, [\, U(\varphi(t),\psi(t),\xi(t))\, ]$](img437.gif) |
||
Iz teorema 2.1 zaključujemo da za cirkulaciju potencijalnog polja uvijek vrijedi
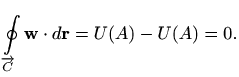
No, vrijedi i obrat koji nam daje još jednu karakterizaciju potencijalnih polja (pored one iz teorema 1.7): na konveksnom skupu
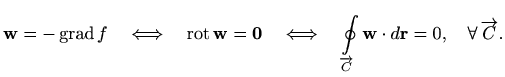
Opišimo kako se nalazi potencijal potencijalnog polja. Iz dokaza teorema 2.1 vidimo da je potencijal polja
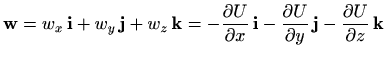
integral totalnog diferencijala,
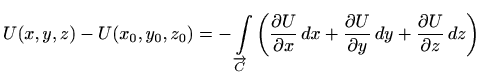
za svaku krivulju
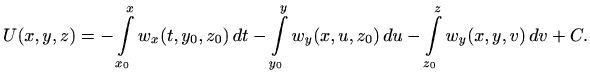
U prethodnoj formuli smo iskoristili činjenicu da je potencijal
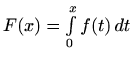 iz [M2, teorem 2.3].
iz [M2, teorem 2.3].
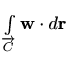 gdje je
gdje je
i
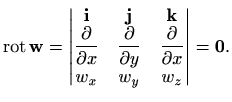
Kako je polje
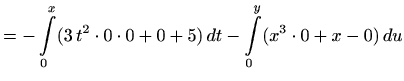 |
||
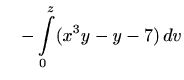 |
||
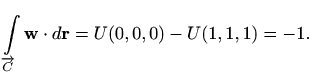
U zadatku b) radi se o cirkulaciji potencijalnog polja pa je
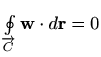 bez obzira na parametre
bez obzira na parametre