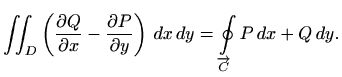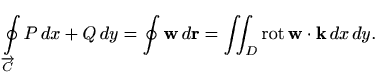Teorem 2.2 [Green]
Neka su
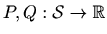
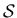 otvoren skup (bez
ruba). Neka je
otvoren skup (bez
ruba). Neka je
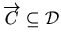 pozitivno orijentirana po
djelovima glatka krivulja i neka je
pozitivno orijentirana po
djelovima glatka krivulja i neka je 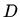 unija krivulje
unija krivulje
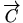 i unurašnjeg
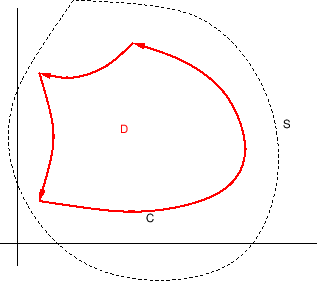
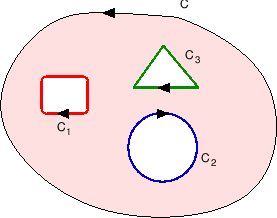
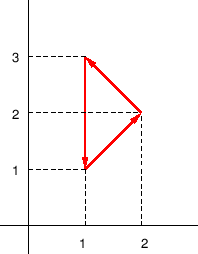
područja kojeg ta krivulja omeđuje (vidi sliku 2.9). Tada je
i unurašnjeg
područja kojeg ta krivulja omeđuje (vidi sliku 2.9). Tada je
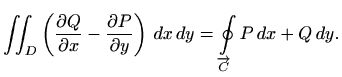
dvije diferencijabilne funkcije, pri čemu je