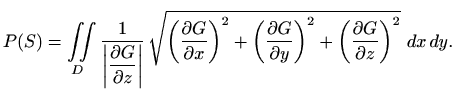jednadžba skupa
Ploha ![]() je glatka u točki
je glatka u točki ![]() ako je funkcija
ako je funkcija ![]() diferencijabilna
u točki
diferencijabilna
u točki ![]() , pri čemu je
, pri čemu je
![]() i
i
![]() .
.
Ploha ![]() je glatka ploha ako je glatka u svakoj točki.
je glatka ploha ako je glatka u svakoj točki.
jednadžba skupa
Ploha ![]() je glatka u točki
je glatka u točki ![]() ako je funkcija
ako je funkcija ![]() diferencijabilna
u točki
diferencijabilna
u točki ![]() , pri čemu je
, pri čemu je
![]() i
i
![]() .
.
Ploha ![]() je glatka ploha ako je glatka u svakoj točki.
je glatka ploha ako je glatka u svakoj točki.
Parametrizacija plohe iz definicije 3.1 prikazana je na slici 3.1.
Važno je primjetiti da ne mora za svaku točku na plohi biti zadan isti
sustav. Tako je, na primjer, na slici 3.2 za točku ![]() funkcija
funkcija ![]() zadana u sustavu
zadana u sustavu
![]() , dok je za točku
, dok je za točku ![]() funkcija
funkcija ![]() zadana u sustavu
zadana u sustavu
![]() .
.
Plohe možemo zadati na razne načine. Ako je čitava ploha ![]() zadana jednom
funkcijom
zadana jednom
funkcijom
![]() , gdje je
, gdje je
![]() , kažemo da je
, kažemo da je
eksplicitna jednadžba plohe.
Na primjer, za
![]() i
i
![]() je
je ![]() implicitna jednadžba hiperboličkog paraboloida (vidi [M2, poglavlje 3.4.2]).
implicitna jednadžba hiperboličkog paraboloida (vidi [M2, poglavlje 3.4.2]).
Ako je skup
![]() otvoren i ako je funkcija
otvoren i ako je funkcija ![]() derivabilna
te je
derivabilna
te je
![]() za svaku točku
za svaku točku ![]() , onda je
, onda je
implicitna jednadžba plohe
Ploha
Na primjer, za
![]() i
i
![]() je
je
![]() implicitna jednadžba plašta
jedinične kugle. Očito je
implicitna jednadžba plašta
jedinične kugle. Očito je
u svakoj točki
Plohu možemo zadati i parametarski:
Na primjer, eksplicitno zadana ploha je specijalan slučaj parametarski zadane plohe uz
Parametarsko zadavanje ploha je najuniverzalniji način zadavanja ploha. Tako, na primjer, elipsoid zadajemo s [M2, poglavlje 3.4]
![$\displaystyle =u \cos u \left(1+\displaystyle \frac{\cos v}{2}\right), \qquad u,v\in [0,2\,\pi],$](img523.gif) |
||
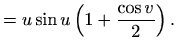 |
6*cos(u)*cos(v), 4*sin(u)*cos(v), 2*sin(v) (1-0.2*cos(v))*cos(u), (1-0.2*cos(v))*sin(u), 0.2*sin(v) cos(v)**3*cos(u)**3, sin(v)**3*cos(u)**3, sin(u)**3 cos(u)*u*(1+cos(v)/2), sin(v)*u/2, sin(u)*u*(1+cos(v)/2)Pri tome za svaku plohu odaberite odgovarajuće granice za parametre
Parametarsku vektorsku jednadžbu plohe ![]() dobijemo kada plohu zadamo
kao hodograf vektorske funkcije:
dobijemo kada plohu zadamo
kao hodograf vektorske funkcije:
Ako se ploha ![]() sastoji od konačno glatkih ploha, a na spojnim krivuljama ne
postoje tangencijalne ravnine, kažemo da je
sastoji od konačno glatkih ploha, a na spojnim krivuljama ne
postoje tangencijalne ravnine, kažemo da je ![]() po dijelovima glatka
ploha. Skup svih točka u kojima ne postoji tangncijalna tavnina ima
površinu nula pa ga kod računanja integrala možemo zanemariti.
Na primjer, ploha na slici 3.3 sastoji se od četiri glatke plohe,
po dijelovima glatka
ploha. Skup svih točka u kojima ne postoji tangncijalna tavnina ima
površinu nula pa ga kod računanja integrala možemo zanemariti.
Na primjer, ploha na slici 3.3 sastoji se od četiri glatke plohe,
![]() ,
, ![]() ,
, ![]() i
i ![]() .
.
Sada možemo definirati površinu plohe.
U prethodnoj definiciji izraz ![]() je element površine, dakle,
površina je jednaka "beskonačnom zbroju" (integral) beskonačno malih elemenata
površine. Objasnimo formulu ze element površine
je element površine, dakle,
površina je jednaka "beskonačnom zbroju" (integral) beskonačno malih elemenata
površine. Objasnimo formulu ze element površine ![]() pomoću slike 3.4.
pomoću slike 3.4.
Dio plohe ![]() koji se projicira na pravokutnik
koji se projicira na pravokutnik
aproksimiramo paralelogramom koji leži u tangencijalnoj ravnini plohe
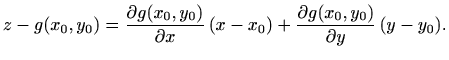
Vrhovi paralelograma su
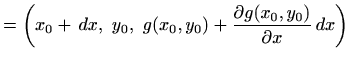 |
||
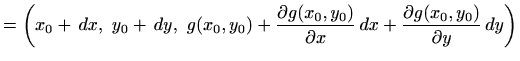 |
||
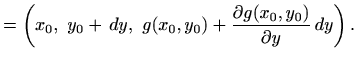 |
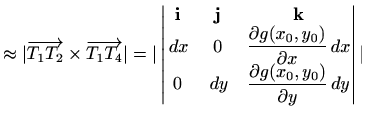 |
||
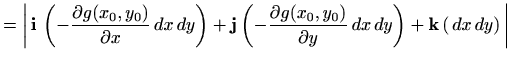 |
||
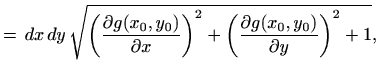 |
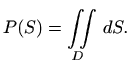
Ako je funkcija ![]() implicitno zadana jednadžbom
implicitno zadana jednadžbom
![]() , onda iz
[M2, poglavlje 3.11, napomena 3.12]
, onda iz
[M2, poglavlje 3.11, napomena 3.12]
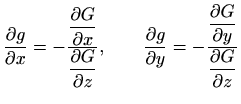
slijedi