×   HOME PREDAVANJA

SADRŽAJ VEKTORSKA ANALIZA KRIVULJNI INTEGRALI PLOŠNI INTEGRALI

PODSJETNIK

SADRŽAJ VEKTORSKA ANALIZA KRIVULNJI INTEGRALI PLOŠNI INTEGRALI

NETPLOT OCTAVE Traži ...

☰   matematika3 Potencijalna i solenoidalna polja     VEKTORSKA ANALIZA     KRIVULJNI INTEGRALI

Usmjerene derivacije

Neka su zadani skup $D\in \mathbb{R}^3$ , točka $T_0\in D$ i vektor $\mathbf{a}$ s hvatištem u točki $T_0$ . Neka je

$$\mathbf{a}_0 =\frac{\mathbf{a}}{\vert\mathbf{a}\vert}$$

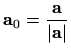
jedinični vektor vektora $\mathbf{a}$ [M1, poglavlje 3.6]. Neka točka $T$ leži na zraci određenoj vektorom $\mathbf{a}$ i neka je

$$\overrightarrow{T_0T}=t\, \mathbf{a}, \qquad t\geq 0.$$

Uz ovakvu deiniciju parametra $t$ očito vrijedi $d(T_0,T)=t$ .

Definicija 1.13   Derivacija skalarnog polja $U:D\to \mathbb{R}$ u točki $T_0$ u smjeru vektora $\mathbf{a}$ je broj

$$\frac{\partial U }{\partial \mathbf{a}}=\lim_{t\to 0} \frac{U(T)-U(T_0)}{t}.$$

Derivacija vektorskog polja $\mathbf{w}:D\to V_0$ u točki $T_0$ u smjeru vektora $\mathbf{a}$ je vektor

$$\frac{\partial \mathbf{w}}{\partial \mathbf{a}}=\lim_{t\to 0} \frac{\mathbf{w}(T)-\mathbf{w}(T_0)}{t}.$$

Sljedeći teorem daje jednostavne formule za računanje usmjerenih derivacija.

Teorem 1.8   Vrijedi

$$\displaystyle \frac{\partial U(T) }{\partial \mathbf{a}} = \mathbf{a}_0 \cdot \mathop{\mathrm{grad}}\nolimits U(T),$$

$$\displaystyle \frac{\partial \mathbf{w}(T) }{\partial \mathbf{a}} = (\mathbf{a}_0\cdot \nabla) \, \mathbf{w}(T).$$

Dokaz.

Dokažimo prvu tvrdnju teorema. Neka u sustavu $(O,\mathbf{i},\mathbf{j}, \mathbf{k})$ vrijedi $T=(x,y,z)$ , $T_0=(x_0,y_0,z_0)$ i $U(T)=U(x,y,z)$ . Tada jednakost

$$\overrightarrow{OT}=\overrightarrow{OT_0}+\overrightarrow{T_0T}$$

zapisujemo kao

$$x\, \mathbf{i}+y\, \mathbf{j} + z\, \mathbf{k} = x_0\, \mathbf{i}+y_0\, \mathbf{j} + z_0\, \mathbf{k} +t\, \mathbf{a}_0$$

$$= (x_0+t\, \mathbf{a}_0 \cdot \mathbf{i}) \, \mathbf{i} + (y_0+t\... ...thbf{j}) \, \mathbf{j} + (z_0+t\, \mathbf{a}_0 \cdot \mathbf{k}) \, \mathbf{k}.$$

Dakle, za svaku točku $T$ na zraci određenoj točkom $T_0$ i vektorom $\mathbf{a}$ vrijedi

$$x=x_0+t\, \mathbf{a}_0 \cdot \mathbf{i},\quad y=y_0+t\, \mathbf{a}_0 \cdot \mathbf{j}, \quad z=z_0+t\, \mathbf{a}_0 \cdot \mathbf{k}.$$

Stoga je limes iz definicije 1.13 u stvari jednak derivaciji funkcije jedne varijable

$$g(t)=f(x_0+t\, \mathbf{a}_0 \cdot \mathbf{i},y_0+t\, \mathbf{a}_0 \cdot \mathbf{j}, z_0+t\, \mathbf{a}_0 \cdot \mathbf{k})$$

u točki $t=0$ . Dakle,

$$\displaystyle \frac{\partial U(T) }{\partial \mathbf{a}}(T_0)=\displaystyle \frac{dg}{dt}\bigg\vert _{t=0} =\left(\displaystyle \frac{\partial f}{\partial x}\,\displaystyle... ...artial z}\,\displaystyle \frac{\partial z}{\partial t} \right)\bigg\vert _{t=0}$$

$$=\left(\displaystyle \frac{\partial f}{\partial x} \, \mathbf{a}_... ...tyle \frac{\partial f}{\partial z} \, \mathbf{a}_0\cdot \mathbf{k} \right)(T_0)$$

$$=\mathbf{a}_0 \cdot \left( \displaystyle \frac{\partial f}{\parti... ...athbf{j} \displaystyle \frac{\partial f}{\partial z}(T_0) \, \mathbf{k} \right)$$

$$=\mathbf{a}_0 \cdot \mathop{\mathrm{grad}}\nolimits U(T_0).$$

Q.E.D.

Primjer 1.6   Neka je zadano

$$f(x,y,z) =x^2+3\, y\, z +5,$$

$$\mathbf{w} =y\,z\, \mathbf{i} + z\, x\, \mathbf{j} + x\, y\, \mathbf{k},$$

$$\mathbf{a} = 2\, \mathbf{i} + \mathbf{j} -2\, \mathbf{k},$$

$$T =(1,-1/2,2).$$

Derivacija skalarnog polja $f$ u smjeru vektora $\mathbf{a}$ glasi

$$\frac{\partial f}{\partial \mathbf{a}}= \mathbf{a}_0 \cdot \matho... ... \mathbf{j} + 3\, y\, \mathbf{k}) = \displaystyle \frac{4}{3}\, x + z -2\, y,$$

pa u točki $T$ imamo

$$\frac{\partial f}{\partial \mathbf{a}}\left(1,-\frac{1}{2},2\right) = \frac{13}{3}.$$

Derivacija vektorskog polja $\mathbf{w}$ u smjeru vektora $\mathbf{a}$ glasi

$$\displaystyle \frac{\partial \mathbf{w}}{\partial \mathbf{a}}= (\mathbf{a}_0\cdot \nabla) \, \mathbf{w} = \displaystyle \frac{2}{3}\, \frac{\partial}{\partial x} (y\,z\, \mathbf{i} + z\, x\, \mathbf{j} + x\, y\, \mathbf{k})$$

$$\quad + \displaystyle \frac{1}{3}\, \frac{\partial}{\partial y} (... ...ial}{\partial z} ( y\,z\, \mathbf{i} + z\, x\, \mathbf{j} + x\, y\, \mathbf{k})$$

$$=\displaystyle \frac{1}{3}\, (z-2\, y) \, \mathbf{i} + \displayst... ...}{3}\, (z-x)\, \mathbf{j} + \displaystyle \frac{1}{3}\, (2\, y-x)\, \mathbf{k},$$

pa u točki $T$ imamo

$$\displaystyle \frac{\partial \mathbf{w}}{\partial \mathbf{a}} \left(1,-\frac{1}{2},2\right) =\mathbf{i} +\frac{2}{3}\, \mathbf{j}.$$

Napomena 1.3   Prema teoremu 1.8 funkcija (skalarno polje) $U$ u danoj točki najbrže raste u smjeru $\mathop{\mathrm{grad}}\nolimits U$ . Naime, izraz [M1, poglavlje 3.9]

$$\mathbf{a}_0 \cdot\mathop{\mathrm{grad}}\nolimits U = \vert\mathb... ...olimits U\vert\, \cos \angle(\mathbf{a}_0,\mathop{\mathrm{grad}}\nolimits U),$$

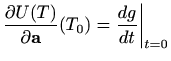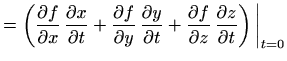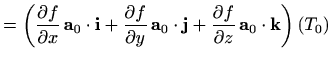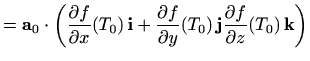poprima najveću vrijednost $\vert\mathop{\mathrm{grad}}\nolimits U\vert$ u kada je $\mathbf{a}_0=(\mathop{\mathrm{grad}}\nolimits U)_0$ jer je tada

$$\cos \angle(\mathbf{a}_0,\mathop{\mathrm{grad}}\nolimits U)=\cos ... ...le((\mathop{\mathrm{grad}}\nolimits U)_0,\mathop{\mathrm{grad}}\nolimits U)=1.$$

Slično razmatranje pokazuje da u danoj točki skalarno polje $U$ najbrže pada u smjeru $-\mathop{\mathrm{grad}}\nolimits U$ jer je onda $\cos \angle(\mathbf{a}_0,\mathop{\mathrm{grad}}\nolimits U)=-1$ .

Napomena 1.4   Vektor normale na nivo-plohu [M2, poglavlje 3.1] funkcije $U(x,y,z)$ u točki $T_0$ dan je s

$$\mathbf{n}_0 =[\mathop{\mathrm{grad}}\nolimits U(T_0)]_0.$$

Naime, jednadžba nivo-plohe u kojoj sve točke imaju vrijednost funkcije jednaku $U(T_0)$ je $U(x,y,z)=U(T_0)$ . Neka je

$$\mathbf{r}=x\,\mathbf{i}+y\,\mathbf{j} + z\,\mathbf{k}, \qquad d\mathbf{r} = dx\,\mathbf{i}+dy\,\mathbf{j} + dz\,\mathbf{k}.$$

Funkcije $U$ je na nivo-plohi konstantna pa vrijedi

$$0=dU(x_0,y_0,z_0)=\frac{\partial U}{\partial x}\, dx + \frac{\pa... ...U}{\partial z}\, dz =\mathop{\mathrm{grad}}\nolimits U(T_0) \cdot d\mathbf{r}.$$

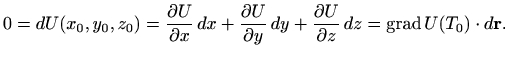
No, pošto smo se ograničili na nivo-plohu, $d\mathbf{r}$ je infinitezimalni pomak po tangencijalnoj ravnini te plohe u točki $T_0$ . Prema prethodnoj jednakosti $\mathop{\mathrm{grad}}\nolimits U(T_0)$ je okomit na $d\mathbf{r}$ pa je stoga kolinearan s vektorom normale, odnosno

$$\mathop{\mathrm{grad}}\nolimits U(T_0) = \lambda \mathbf{n}_0, \qquad \lambda\in \mathbb{R}, \quad \lambda \neq 0.$$

Potencijalna i solenoidalna polja     VEKTORSKA ANALIZA     KRIVULJNI INTEGRALI