 |
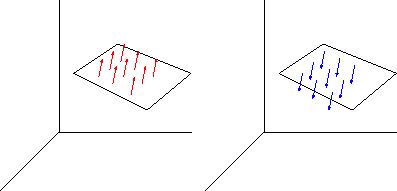
Orijentaciju plohe u danoj točki definiramo kao orijentaciju normale tangencijalne ravnine u toj točki - svaka točka ima dvije moguće orijentacije. Zanimaju nas samo dvostrane plohe, odnosno plohe koje imaju dvije neprekidne orijentacije (vidi sliku 3.6).
Primjer jednostrane plohe koja nema dvije već samo jednu neprekidnu orijentaciju je Möbiusova vrpca prikazana na slici 3.7.
Parametarska jednadžba Möbiusove vrpce poluširine ![]() i središnje kružnice
radijusa
i središnje kružnice
radijusa ![]() je
je
Möbiusova vrpca se koristi kod konvejerskih traka kako bi se "obje" strane podjednako trošile i kod vrpca za beskonačno snimanje pri čemu se ujedno udvostručuje kapacitet snimanja.
Kod po dijelovima glatkih ploha sve dijelove moramo orijentirati suglasno kako je prikazano na slici 3.8.
Kod zatvorenih ploha (na primjer, sfera) imamo vanjsku i unutrašnju orijentaciju (vidi sliku 3.9).
Jedna od neprekidnih orijentacija dvostrane plohe ![]() zadane jednadžbom
zadane jednadžbom
je dana poljem jediničnih vektora normale,
Koristeći definicije polja jediničnih normala
![]() i elementa površine
i elementa površine
![]() , uz oznaku
, uz oznaku
možemo pisati
Plošni integral vektorskog polja
po po djelovima glatkoj plohi
![]() sastavljenoj od suglasno orijentiranih
ploha
sastavljenoj od suglasno orijentiranih
ploha
![]() definiramo kao
definiramo kao
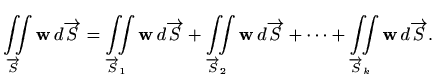
U fizici se
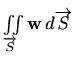 zove tok ili
fluks vektorskog polja
zove tok ili
fluks vektorskog polja
![]() kroz plohu
kroz plohu
![]() .
.
Bez dokaza navodimo sljedeće tvrdnje:
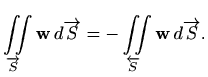
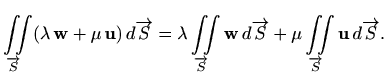
Polje jediničnih normala
![]() možemo izraziti i pomoću kosinusa
smjerova
možemo izraziti i pomoću kosinusa
smjerova
![]() [M1, poglavlje 3.6],
[M1, poglavlje 3.6],
pri čemu su
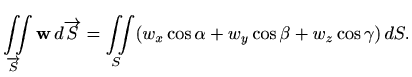
Koristeći formulu (3.1) za
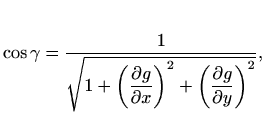
pa je
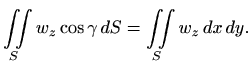
No, ako plohu
onda je
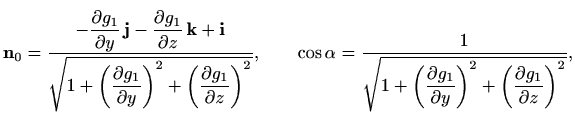
pa je
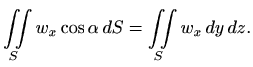
Slično, ako plohu
onda je
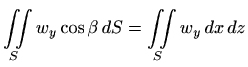
pa imamo
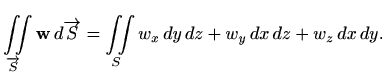
Kod primjene ove formule još treba ispravno odrediti predznak integrala:
a u protivnom će predznak biti "
Kako smo u izvodu prethodne formule zadanu plohu projicirali na tri koordinatne ravnine, plošni integral vekorskog polja još zovemo i integral po projekcijama. Uz oznake (2.1) iz prethodnih formula slijedi
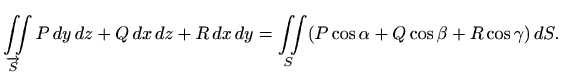
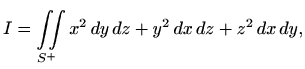
gdje je
Vidimo da se oba dijela plohe, ![]() i
i ![]() projiciraju na isti skup
projiciraju na isti skup ![]() u
u
![]() -ravnini vrijedi
-ravnini vrijedi
Za plohu ![]() vrijedi (uz
vrijedi (uz ![]() )
)
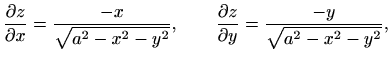
i
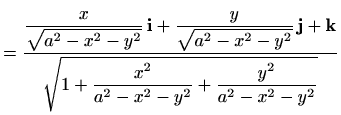 |
||
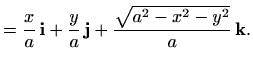 |
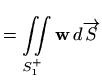 |
||
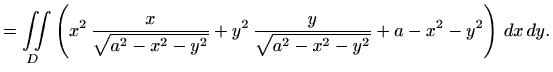 |
Za plohu ![]() vrijedi
vrijedi
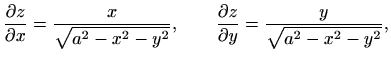
pa je
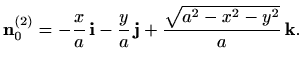
No, kako nam je potrebna vanjska normala plohe
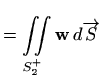 |
||
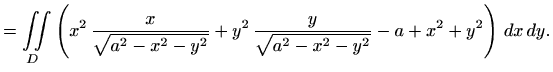 |
![$\displaystyle =I_1+I_2 = 2\, \iint\limits_D \displaystyle \frac{x^3+y^3} {\sqrt...
... \varphi ,&\varphi \in[0,\pi] \\ y=r\sin\varphi ,&r\in[0,a] \end{array}\right\}$](img658.gif) |
||
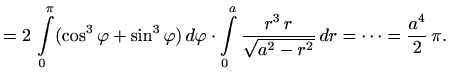 |
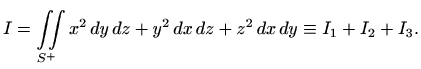
Za integral
Za polovicu polusfere za koju je ![]() uzimamo predznak "
uzimamo predznak "![]() " jer je ku
vanjske normale s vektorom
" jer je ku
vanjske normale s vektorom
![]() manji ili jednak
manji ili jednak ![]() , a za polovicu
plosfere za koju je
, a za polovicu
plosfere za koju je ![]() uzimamo predznak "
uzimamo predznak "![]() " (vidi sliku
3.10) pa uz
" (vidi sliku
3.10) pa uz
![]() vrijedi
vrijedi
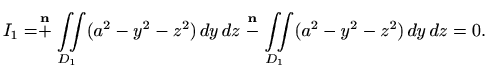
Analogno, za ![]() imamo
imamo
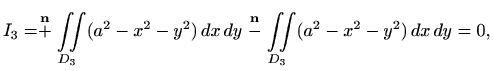
gdje je
Za ![]() se cijela ploha
se cijela ploha ![]() projicira na središnji krug radijusa
projicira na središnji krug radijusa ![]() u
u
![]() -ravnini. Predznak integrala je "
-ravnini. Predznak integrala je "![]() " jer vanjska normala zatvara s
vektorom
" jer vanjska normala zatvara s
vektorom
![]() kut manji ili jednak
kut manji ili jednak ![]() (vidi sliku 3.10).
Iz
(vidi sliku 3.10).
Iz
![]() konačno imamo
konačno imamo
![$\displaystyle =I_2= \stackrel{\mathbf{n}}{+} \iint\limits_{D_2} (a^2-x^2-z^2) \...
...rphi ,&\varphi \in[0,2\, \pi] \\ z=r\sin\varphi ,&r\in[0,a] \end{array}\right\}$](img671.gif) |
||
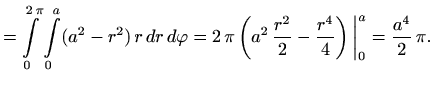 |