☰ matematika3

Plošni integral vektorskog polja PLOŠNI INTEGRALI Stokesova formula

Teoremi o divergenciji, gradijentu i rotoru

Cirkulaciju vektorskog polja $\mathbf{w}$ kroz zatvorenu orijentiranu plohu označavamo s

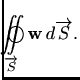
$\displaystyle \bigcirc \hspace{-0.55cm} \int \hspace{-0.28cm} \int \limits_{\overrightarrow{S}} \mathbf{w} \, d\overrightarrow{S}.$

Zatvorenu plohu koja omeđuje zatvoreno područje $V\subseteq \mathbb{R}^3$ (rub područja ) označavamo s $\partial V$ odnosno s $\overrightarrow{\partial V}$ ukoliko je ploha orijentirana.

Teorem 3.1 [Teorem o divergenciji, Gauss-Ostrogradski formula] Neka je $\mathbf{w}:V'\to V_0$ neprekidno diferencijabilno vektorsko polje i neka je $V\subseteq V'\subseteq R^3$ zatvoreno područje omeđeno s po dijelovima glatkom plohom $\partial V$ (koja ne presijeca samu sebe). Neka je ploha $\overrightarrow{\partial V}$ orijentirana poljem vanjskih normala. Tada vrijedi

$\displaystyle \iiint\limits_V \mathop{\mathrm{div}}\nolimits \mathbf{w} \, dV =... ...int \limits_{\overrightarrow{\partial V}} \mathbf{w} \cdot \mathbf{n}_0 \, dS.$

Teorem 3.1 daje jedno poopćenje Greenovog teorema na trodimenzionalni slučaj. Naime, u dvodimenzionalnom prostoru Greenovu formulu iz teorema 2.2,

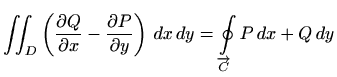
$\displaystyle \iint_D \left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right)\, dx\, dy= \oint\limits_{\overrightarrow{C}}P\, dx+Q\, dy$

možemo neformalno interpretirati kao:

$\textstyle \parbox{6cm}{integral ''derivacije'' po plohi \\ omeđenoj zatvorenom krivuljom}$ = $\textstyle \parbox{5cm}{cirkulacija po orijentiranoj\\ krivulji koja omeđuje plohu}$

Analogno, Gauss-Ostrogradski formulu možemo interpretirati kao

$\textstyle \parbox{6cm}{integral ''derivacije'' po volumenu \\ omeđenom zatvorenom plohom}$ = $\textstyle \parbox{5cm}{cirkulacija po orijentiranoj\\ plohi koja omeđuje volumen}$

Uz oznake

$\displaystyle \mathbf{w}= P\,\mathbf{i} + Q\, \mathbf{j}+R\, \mathbf{k}, \qquad... ...s \alpha \, \mathbf{i} + \cos \beta \, \mathbf{j} + \cos \gamma \, \mathbf{k},$

teorem 3.1 možemo pisati u skalarnoj formi:

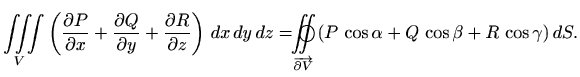
$\displaystyle \iiint\limits_V \left(\frac{\partial P}{\partial x}+ \frac{\parti... ...htarrow{\partial V}} (P\, \cos \alpha + Q\, \cos\beta +R\, \cos\gamma) \, dS.$

Primjer 3.3 Izračunajmo

$\displaystyle I=\bigcirc \hspace{-0.55cm} \int \hspace{-0.28cm} \int \limits_{\overrightarrow{S}} x^3\, dy\, dz+ y^3\, dx\, dz+ z^3\, dx\, dy,$

gdje je $\overrightarrow{S}$ sfera

orijentirana poljem vanjskih normala. Iz

$\displaystyle \mathbf{w}=x^3\,\mathbf{i} + y^3\,\mathbf{j} + z^3\,\mathbf{k},\qquad \mathop{\mathrm{div}}\nolimits \mathbf{w} = 3\,x^2+3\,y^2+3\,z^2,$

primjenom Gauss-Ostrogradski formule i prelaskom na sferne koordinate imamo

$\displaystyle I$	$\displaystyle =\iiint\limits_V (3\,x^2+3\,y^2+3\,z^2 )\, dx\, dy\, dz= \left\{\... ...[0,\pi] \\ z=r\cos \theta & r\in[0,a] \\ J=r^2\sin \theta & \end{array}\right\}$
	$\displaystyle =3\, \int\limits_0^{2\,\pi} \, d\varphi \, \int\limits_0^{\pi} \s... ...\, \int\limits_0^a r^2 \cdot r^2\, dr= \displaystyle \frac{12}{5}\, \pi \, a^5.$

Primjer 3.4 Izračunajmo

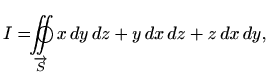
$\displaystyle I=\bigcirc \hspace{-0.55cm} \int \hspace{-0.28cm} \int \limits_{\overrightarrow{S}} x \, dy\, dz+ y \, dx\, dz+ z \, dx\, dy,$

gdje je

proizvoljna po djelovima glatka zatvorena ploha koja omeđuje područje $V\subseteq \mathbb{R}^3$ , a orijentirana je poljem vanjskih normala. Vrijedi

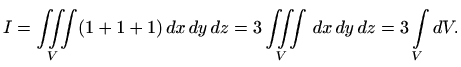
$\displaystyle I=\iiint\limits_V (1+1+1 )\, dx\, dy\, dz= 3 \iiint\limits_V \, dx\, dy\, dz= 3 \int\limits_V dV .$

Dakle, volumen područja

jednak je

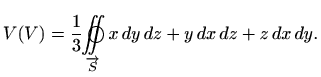
$\displaystyle V(V)= \frac{1}{3} \bigcirc \hspace{-0.55cm} \int \hspace{-0.28cm} \int \limits_{\overrightarrow{S}} x \, dy\, dz+ y \, dx\, dz+ z \, dx\, dy.$

Ova formula je poopćenje korolara 2.1 za

Kao što smo već kazali, Teorem o divergenciji daje vezu dvostrukog integrala po plohi i trostrukog integrala "derivacije" po području omeđenom tom plohom. Imamo još dvije slične veze. Definirajmo integrale

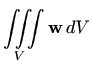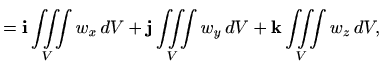$\displaystyle \iiint\limits_V \mathbf{w} \, dV$	$\displaystyle = \mathbf{i} \iiint\limits_V w_x\, dV + \mathbf{j} \iiint\limits_V w_y\, dV + \mathbf{k} \iiint\limits_V w_z\, dV,$
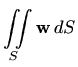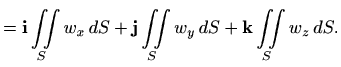$\displaystyle \iint\limits_S \mathbf{w} \, dS$	$\displaystyle = \mathbf{i} \iint\limits_S w_x\, dS + \mathbf{j} \iint\limits_S w_y\, dS + \mathbf{k} \iint\limits_S w_z\, dS.$

U iskazima sljedeća dva teorema je područje omeđeno s po dijelovima glatkom plohom $\partial V$ , a $\mathbf{n}_0$ je polje vanjskih normala.

Teorem 3.2 [Teorem o gradijentu] Vrijedi

$\displaystyle \iiint\limits_V \mathop{\mathrm{grad}}\nolimits f \, dV$	$\displaystyle = \bigcirc \hspace{-0.55cm} \int \hspace{-0.28cm} \int \limits_{\partial V} f\, \mathbf{n}_0 \, dS$
	$\displaystyle = \mathbf{i} \bigcirc \hspace{-0.55cm} \int \hspace{-0.28cm} \int... ...ce{-0.55cm} \int \hspace{-0.28cm} \int \limits_{\partial V} f\cos \gamma \, dS.$

Teorem 3.3 [Teorem o rotaciji] Vrijedi

$\displaystyle \iiint\limits_V \mathop{\mathrm{rot}}\nolimits \mathbf{w} \, dV =... ...ace{-0.28cm} \int \limits_{\partial V} (\mathbf{n}_0 \times \mathbf{w}) \, dS.$

Plošni integral vektorskog polja PLOŠNI INTEGRALI Stokesova formula