Definicija 1.12 Vektorsko polje
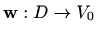 je potencijalno ili konzervativno ako postoji skalarno polje
je potencijalno ili konzervativno ako postoji skalarno polje 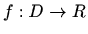 takvo da
je1.2
takvo da
je1.2
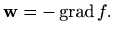
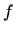 je potencijal polja
je potencijal polja
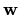 .
Polje
.
Polje
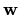 je bezvrtložno ako je
je bezvrtložno ako je
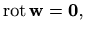
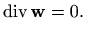
Polje
a solenoidalno ako je
Polje
a solenoidalno ako je
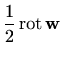 kutna brzina te točke. Stoga
kutna brzina te točke. Stoga
gdje je
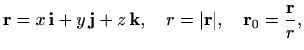
je potencijalno polje s potencijalom
Imamo sljedeći važan teorem.