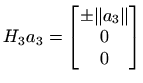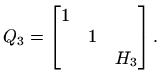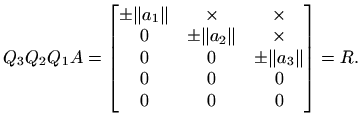Natrag: QR rastav vektora
Gore: QR RASTAV
Naprijed: Numeričko računanje QR
QR rastave matrice nalazimo rekurzivnom primjenom QR rastava vektora.
Postupak ćemo ilustrirati na matrici tipa 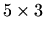 .
Neka je
.
Neka je 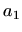 prvi stupac matrice
prvi stupac matrice 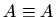 i neka je
QR rastav vektora
i neka je
QR rastav vektora 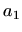 izračunat prema postupku opisanom uz
prethodnom poglavlju. Stavimo
izračunat prema postupku opisanom uz
prethodnom poglavlju. Stavimo 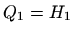 . Tada je
(matrica
. Tada je
(matrica 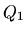 je simetrična)
Neka je
je simetrična)
Neka je 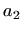 prvi stupac matrice
prvi stupac matrice 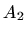 koja je tipa
koja je tipa 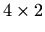 i neka je
QR rastav vektora
i neka je
QR rastav vektora 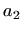 . Stavimo
Tada je
pri čemu je matrica
. Stavimo
Tada je
pri čemu je matrica 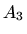 tipa
tipa 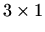 .
Konačno, neka je
.
Konačno, neka je 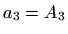 i neka je
QR rastav matrice (vektora)
i neka je
QR rastav matrice (vektora) 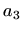 . Stavimo
Tada je
Zbog ortogonalnosti i simetričnosti matrica
. Stavimo
Tada je
Zbog ortogonalnosti i simetričnosti matrica 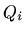 ,
, 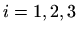 , za
matricu
, za
matricu
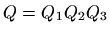 vrijedi
pa sam tako dobili QR rastav matrice
vrijedi
pa sam tako dobili QR rastav matrice  .
.
Ovaj postupak se lako može poopćiti na matricu bilo koje dimenzije.



Natrag: QR rastav vektora
Gore: QR RASTAV
Naprijed: Numeričko računanje QR
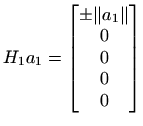
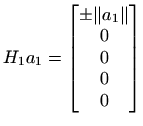
![$\displaystyle Q_1 A = \left[ \begin{array}{c\vert c}
\pm \Vert a_1\Vert & \begi...
...\\
\hline \begin{array}{c}0 0 0 0\end{array} &
A_2
\end{array}\right].
$](img150.gif)
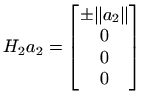
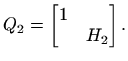
![\begin{displaymath}
Q_2 Q_1 A = \left[ \begin{array}{cc\vert c}
\begin{array}{c}...
...gin{array}{c}0 0 0
\end{array}& A_3
\end{array} \right]
\end{displaymath}](img156.gif)