U ovom poglavlju definirat ćemo pojmove dužine, usmjerene dužine i
vektora te navesti osnovno svojstvo trodimenzionalnog Euklidskog prostora
![]() .
Pretpostavljamo da su pojmovi kao što su pravac, ravnina, kut i
prostor poznati.
.
Pretpostavljamo da su pojmovi kao što su pravac, ravnina, kut i
prostor poznati.
Usmjerena dužina
![]() je dužina kod koje su rubne točke uređene,
odnosno točka
je dužina kod koje su rubne točke uređene,
odnosno točka ![]() je početak ili
hvatište, a
točku
je početak ili
hvatište, a
točku ![]() svršetak. Udaljenost točaka
svršetak. Udaljenost točaka ![]() i
i ![]() se
u ovom slučaju zove duljina (norma ili
intenzitet)
usmjerene dužine
se
u ovom slučaju zove duljina (norma ili
intenzitet)
usmjerene dužine
![]() i označava s
i označava s
![]() .
.
Usmjerene dužine
![]() i
i
![]() su ekvivalentne, odnosno
su ekvivalentne, odnosno
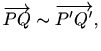
ako dužine
Vektor je klasa ekvivalencije usmjerenih dužina. Vektore označavamo s
Ako je usmjerena dužina
Nul-vektor
je vektor koji ima početak i kraj u istoj točki. Nul-vektor
označavamo s
![]() , vrijedi
, vrijedi
![]() , a njegovi
predstavnici su sve usmjerene dužine oblika
, a njegovi
predstavnici su sve usmjerene dužine oblika
![]() .
.
Dokažimo da je relacija ![]() iz definicije 3.1 zaista
relacija ekvivalencije. Prema definiciji 1.4,
relacija ekvivalencije
je refleksivna, simetrična i tranzitivna.
Očito je
iz definicije 3.1 zaista
relacija ekvivalencije. Prema definiciji 1.4,
relacija ekvivalencije
je refleksivna, simetrična i tranzitivna.
Očito je
![]() pa je relacija
pa je relacija
![]() refleksivna. Također, ako je
refleksivna. Također, ako je
![]() , tada je i
, tada je i
![]() pa je relacija
pa je relacija
![]() simetrična.
Dokaz tranzitivnosti je nešto složeniji.
Ukoliko točke
simetrična.
Dokaz tranzitivnosti je nešto složeniji.
Ukoliko točke ![]() ,
, ![]() ,
, ![]() i
i ![]() ne leže na istom pravcu, tada je
ne leže na istom pravcu, tada je
![]() ako i samo ako
su točke
ako i samo ako
su točke ![]() susjedni vrhovi paralelograma
(vidi sliku 3.1).
Ukoliko točke
susjedni vrhovi paralelograma
(vidi sliku 3.1).
Ukoliko točke ![]() ,
, ![]() ,
, ![]() i
i ![]() leže na istom pravcu, tada je
leže na istom pravcu, tada je
![]() ako i samo ako
vrijedi
ako i samo ako
vrijedi
U ovom slučaju kažemo da su točke
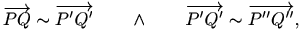
tada su točke
Vezu između usmjerenih dužina i vektora daje nam
osnovno svojstvo euklidskog prostora:
ako je
![]() proizvoljna točka i
proizvoljna točka i
![]() zadani vektor,
tada postoji jedinstvena točka
zadani vektor,
tada postoji jedinstvena točka ![]() takva da je usmjerena dužina
takva da je usmjerena dužina
![]() predstavnik vektora
predstavnik vektora
![]() .
S ovim postupkom je vektor
.
S ovim postupkom je vektor
![]() sveden na početak
sveden na početak ![]() odnosno
nanesen na
odnosno
nanesen na ![]() . U primjenama često pišemo i
. U primjenama često pišemo i
Premda taj zapis nije sasvim korektan jer je vektor
Vektori
Iz definicije slijedi da su dva vektora jednaka ako su kolinearni, istog smjera i jednake duljine. Posebno, nul-vektor je kolinearan sa svakim vektorom i za njega nema smisla govoriti o orijentaciji.