☰
matematika1
Osnove matematike
Vektorska algebra i analitička
Linearna algebra
- 1.
-
![[*]](../icons.gif/crossref.gif) Što je sustav linearnih jednadžbi?
Što je sustav linearnih jednadžbi?
- 2.
-
![[*]](../icons.gif/crossref.gif) Što je matrica?
Što je matrica?
![[*]](../icons.gif/crossref.gif) Kako zbrajamo matrice?
Kako zbrajamo matrice?
![[*]](../icons.gif/crossref.gif)
![[*]](../icons.gif/crossref.gif) Kako množimo matrice?
Kako množimo matrice?
- 3.
-
![[*]](../icons.gif/crossref.gif) Što je jedinična matrica; nul-matrica;
Što je jedinična matrica; nul-matrica;
![[*]](../icons.gif/crossref.gif) transponirana matrica; simetrična matrica?
transponirana matrica; simetrična matrica?
- 4.
- Kako pomoću matrice zapisujemo
sustav linearnih jednadžbi?
![[*]](../icons.gif/crossref.gif)
- 5.
-
![[*]](../icons.gif/crossref.gif) Kako rješavamo trokutaste sustave?
Kako rješavamo trokutaste sustave?
![[*]](../icons.gif/crossref.gif) Opišite postupak Gaussove eliminacije.
Opišite postupak Gaussove eliminacije.
![[*]](../icons.gif/crossref.gif) Što je pivotiranje?
Što je pivotiranje?
- 6.
-
![[*]](../icons.gif/crossref.gif) Kada su vektori linearno nezavisni?
Kada su vektori linearno nezavisni?
![[*]](../icons.gif/crossref.gif) Kako definiramo rang matrice?
Kako definiramo rang matrice?
![[*]](../icons.gif/crossref.gif) Kako određujemo rang matrice?
Kako određujemo rang matrice?
- 7.
- Kada kažemo da su dvije matrice ekvivalentne
![[*]](../icons.gif/crossref.gif) i što
vrijedi u tom slučaju?
i što
vrijedi u tom slučaju?
![[*]](../icons.gif/crossref.gif)
- 8.
-
![[*]](../icons.gif/crossref.gif) Kako glasi Kronecker-Capellijev teorem?
Dokažite da je sustav
Kako glasi Kronecker-Capellijev teorem?
Dokažite da je sustav
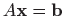 rješiv ako i samo ako je
rješiv ako i samo ako je
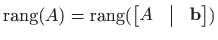 .
.
![[*]](../icons.gif/crossref.gif)
- 9.
-
![[*]](../icons.gif/crossref.gif) Što je inverzna matrica?
Dokažite da je inverzna matrica
jedinstvena ako postoji. Dokažite da je
Što je inverzna matrica?
Dokažite da je inverzna matrica
jedinstvena ako postoji. Dokažite da je
- 10.
- Opišite postupak traženja
inverzne matrice.
![[*]](../icons.gif/crossref.gif)
- 11.
- Dokažite da je matrica
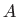 reda
reda 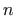 regularna ako i samo ako
je
regularna ako i samo ako
je
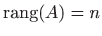 .
.
![[*]](../icons.gif/crossref.gif)
- 12.
- Definirajte slijedeće pojmove: permutacija, inverzija,
parnost.
![[*]](../icons.gif/crossref.gif)
- 13.
- Što je determinanta?
![[*]](../icons.gif/crossref.gif)
- 14.
- Navedite i dokažite svojstva determinanti:
![[*]](../icons.gif/crossref.gif)
- a)
- determinanta trokutaste matrice jednaka je produktu elemenata
na dijagonali,
- b)
-
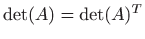 ,
,
- c)
- zamjenom dvaju stupaca (redaka) determinanta mijenja
predznak,
- d)
- determinanta matrice s dva jednaka stupca (retka) jednaka je
nuli,
- e)
- determinanta je linearna funkcija svojih stupaca (redaka),
- f)
- ako determinanta ima nul stupac (redak), onda je jednaka
nuli,
- g)
- determinanta se ne mijenja ako nekom stupcu (retku) pribrojimo
neki drugi stupac (redak) pomnožen nekim brojem,
- h)
-
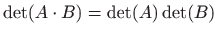 ako obje determinante na desnoj
strani postoje (bez dokaza).
ako obje determinante na desnoj
strani postoje (bez dokaza).
- 15.
- Dokažite da su lijedeće tvrdnje ekvivalentne:
- a)
-
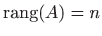 ,
,
- b)
-
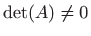 ,
,
- c)
- postoji
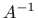 .
.
- 16.
- Kako možemo definirati rang pomoću poddeterminanti?
![[*]](../icons.gif/crossref.gif)
- 17.
- Objasnite Laplaceov razvoj determinante:
![[*]](../icons.gif/crossref.gif)
- 18.
- Objasnite i dokažite formulu
![[*]](../icons.gif/crossref.gif)
- 19.
- Izrecite i dokažite Cramerovo pravilo.
![[*]](../icons.gif/crossref.gif)
Osnove matematike
Vektorska algebra i analitička
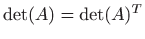 ,
,
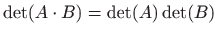 ako obje determinante na desnoj
strani postoje (bez dokaza).
ako obje determinante na desnoj
strani postoje (bez dokaza).
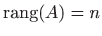 ,
,
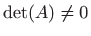 ,
,
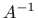 .
.