Iz prikaza (2.1) vidimo da zadnjih ![]() stupaca matrice
stupaca matrice ![]() ne
sudjeluje kod računanja produkta
ne
sudjeluje kod računanja produkta ![]() jer se množe s nulom.
Stoga
jer se množe s nulom.
Stoga ![]() rastav
rastav ![]() možemo u ekonomičnom obliku zapisati kao
možemo u ekonomičnom obliku zapisati kao
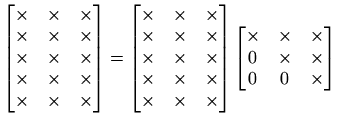
[Q,R]=qr(A,0) daje ekonomični QR rastav
matrice
Octave On-line[Octave On-line Home] [Octave User's Guide] |