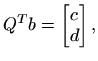
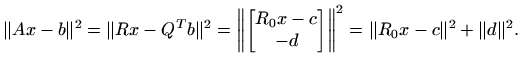
Slijedeći Matlab potprogram rješava problem najmanjih kvadrata pomoću QR rastava:
function x=LS(A,b) % Rjesava problem najmanjih kvadrata || Ax-b || --> min % za matricu punog stupcanog ranga A koristeci QR rastav. [m,n]=size(A); [Q,R]=moj_QR(A); b1=Q'*b; c=b1(1:n); x=R(1:n,1:n)\c; end
x=A\b.
Octave On-line[Octave On-line Home] [Octave User's Guide] |