

Next: Finite Dimensional Case
Up: An Upper Bound for
Previous: Review of the Minimum
Calculaton of 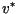 is on firm ground when the matrices involved are finite.
For the fungal problem, however, the matrices concerned are infinite
dimensional and calculation of the
maximum eigenvalue of
is on firm ground when the matrices involved are finite.
For the fungal problem, however, the matrices concerned are infinite
dimensional and calculation of the
maximum eigenvalue of
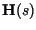 is not straightforward. Recalling that we
have taken
is not straightforward. Recalling that we
have taken  to be the (scalar) moment generating function for the
dispersal kernel
to be the (scalar) moment generating function for the
dispersal kernel 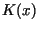 , and taking
, and taking 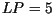 to be definite, we can write
to be definite, we can write
 |
(17) |
where 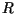 is defined by (5).
is defined by (5).
In order to analyze the spectrum of  , we consider the linear operator
, we consider the linear operator
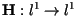 defined by
defined by
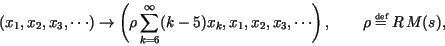 |
(18) |
where 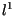 is the Banach space of all real sequences
is the Banach space of all real sequences
 such that
such that
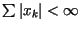 .
The matrix
.
The matrix 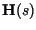 is the representation of
is the representation of 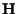 in the standard basis
in the standard basis
 , where
, where 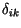 is the
Kronecker symbol. Our choice of the space
is the
Kronecker symbol. Our choice of the space 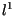 is natural, since the total number of
lesions and spores is always finite.
The domain of
is natural, since the total number of
lesions and spores is always finite.
The domain of 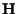 is
is
which also reflects the previous natural assumption, since the summation in
the definition in the domain is proportional to the total number of spores
produced (large, but finite).
The operator  is unbounded, invertible, and its inverse is the
left-shift operator
is unbounded, invertible, and its inverse is the
left-shift operator
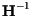 defined by
defined by
Clearly,
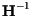 is bounded, so
is bounded, so  is a closed operator, and we can
use classical analysis of closed operators (see [2, §2.6 and §2.7]).
For each
is a closed operator, and we can
use classical analysis of closed operators (see [2, §2.6 and §2.7]).
For each  , the operator
, the operator
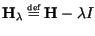 is
defined by
is
defined by
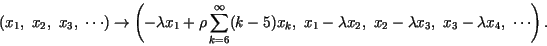 |
(19) |
The point spectrum of  is the set
is the set
 of all points
of all points
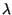 for which
for which
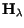 has no inverse. Each element of
has no inverse. Each element of
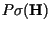 is the eigenvalue of
is the eigenvalue of  . For each eigenvalue
. For each eigenvalue 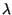 ,
each
,
each
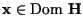 such that
such that
 , is the
corresponding eigenvector. Thus, equating the right hand side of (19) to zero
gives
, is the
corresponding eigenvector. Thus, equating the right hand side of (19) to zero
gives
 |
(20) |
For the first component, by using (20) and induction, we have
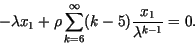 |
(21) |
From (20) it follows that any non-trivial solution of
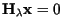 must satisfy
must satisfy  , so
(21) implies
, so
(21) implies
Since we are looking for the largest eigenvalue, we confine ourselves to the
case  . By using differentiation of geometric series, we have
. By using differentiation of geometric series, we have
Therefore, the eigenvalues of 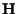 are the zeros of the polynomial
are the zeros of the polynomial
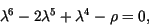 |
(22) |
which also satisfy  .
From (20) we see that the corresponding eigenvectors are
.
From (20) we see that the corresponding eigenvectors are
It is obvious that
 , but since
, but since 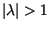 also implies
also implies
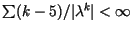 , we also have
, we also have
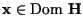 .
Interestingly, the roots of the polynomial (22) can be computed exactly
in terms of
radicals (e.g. by Mathematica), and they all lie outside the unit
circle. Inspecting all six roots, we see that the largest magnitude root of
the
polynomial (22) is
.
Interestingly, the roots of the polynomial (22) can be computed exactly
in terms of
radicals (e.g. by Mathematica), and they all lie outside the unit
circle. Inspecting all six roots, we see that the largest magnitude root of
the
polynomial (22) is
 |
(23) |
Since in deriving this expression we have assumed that 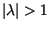 ,
we conclude that (23) gives the largest eigenvalue of the operator
,
we conclude that (23) gives the largest eigenvalue of the operator
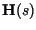 from (17). Since
from (17). Since  , expression (23), together with (10), allows
for prediction of rates of invasion as a function of parameters describing the
fecundity,
dispersal, and infectiousness of P. infestans. In addition, since the maximum eigenvalue
, expression (23), together with (10), allows
for prediction of rates of invasion as a function of parameters describing the
fecundity,
dispersal, and infectiousness of P. infestans. In addition, since the maximum eigenvalue  behaves
like
behaves
like 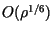 from (23), we also conclude that the predicted
upper bound
from (23), we also conclude that the predicted
upper bound 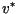 from (10) is stable in the sense that small
changes of the parameters from Table 1 or entries in the matrix cause only small changes in
from (10) is stable in the sense that small
changes of the parameters from Table 1 or entries in the matrix cause only small changes in
 .
.


Next: Finite Dimensional Case
Up: An Upper Bound for
Previous: Review of the Minimum
James Powell, Ivan Slapnicar and Wopke van der Werf
2002-06-01
![]() is on firm ground when the matrices involved are finite.
For the fungal problem, however, the matrices concerned are infinite
dimensional and calculation of the
maximum eigenvalue of
is on firm ground when the matrices involved are finite.
For the fungal problem, however, the matrices concerned are infinite
dimensional and calculation of the
maximum eigenvalue of
![]() is not straightforward. Recalling that we
have taken
is not straightforward. Recalling that we
have taken ![]() to be the (scalar) moment generating function for the
dispersal kernel
to be the (scalar) moment generating function for the
dispersal kernel ![]() , and taking
, and taking ![]() to be definite, we can write
to be definite, we can write
![]() , we consider the linear operator
, we consider the linear operator
![]() defined by
defined by
![]() is bounded, so
is bounded, so ![]() is a closed operator, and we can
use classical analysis of closed operators (see [2, §2.6 and §2.7]).
For each
is a closed operator, and we can
use classical analysis of closed operators (see [2, §2.6 and §2.7]).
For each ![]() , the operator
, the operator
![]() is
defined by
is
defined by