next up previous
Next: Numerical Tests Up: An Upper Bound for Previous: Determination of Maximum Eigenvalue

Finite Dimensional Case

In general one may therefore expect speeds of the nonlinear invasion, governed by the infinite system (2), to approach speeds predicted for the linear system, (6), using the minimum-speed methodology from the previous sections. An additional, new, wrinkle occurs because of the age structure: invasions are initialized with lesions of age 1, and the actual dynamic progress of the disease is modelled by application of finite operators, whose number of entries grows by one for each day following the inception of the invasion. Consequently, when considering the observability of the predicted wave speed there are two convergence issues to consider. The first is the traditional issue concerning the rate at which nonlinear fronts of fixed dimensionality approach the minimal wave speed. The second, novel issue concerns the rate at which the finite dimensional eigenvalue, presumably controlling the speed of propagation in the age-structured population, approaches the largest eigenvalue in the infinite system.

Let $\textbf{H}_m(s)$ be the leading $m \times m$ submatrix of $\textbf{H} (s)$ from (17), where $\rho $ is defined by (18). Let $\lambda _1^{(m)}(s)$ denote the largest positive eigenvalue of $\textbf{H}_m(s)$. To estimate effect of reduction to finite dimension for the linearized case, we need to compute $\lambda _1^{(m)}(s)$, and compare it to $\lambda _1(s)$. First, since $\textbf{H}_m(s)$ is non-negative and irreducible, by the Perron-Frobenius Theorem [14, Theorem 9.2.1] it follows that the absolutely largest eigenvalue of $\textbf{H}_m(s)$ is real and positive. Thus $\lambda _1^{(m)}(s)$ exists for every $m$ and it is equal to the spectral radius of $\textbf{H}_m(s)$. For example, Figure 2 shows the eigenvalues of $\textbf {H}_{100}(s)$ for $\rho =10$. In Figure 2 we see six distinct eigenvalues (there are five distinct eigenvalues for odd $m$), and the rest of the eigenvalues are close to the outer border of the unit circle.

Figure 2: Eigenvalues of $\textbf {H}_{100}(s)$ for $\rho =10$. Note the six eigenvalues outside the unit circle, converging to the six roots of the polynomial $\lambda ^6-2\lambda ^5+\lambda ^4-\rho =0$ in the infinite case.
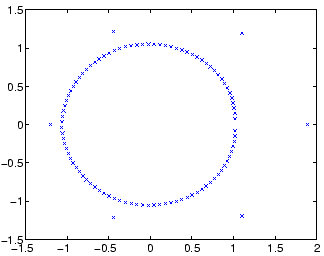
\begin{figure}\begin{center} \epsfig{file=eig100.eps, width=0.45\textwidth}\end{center}\end{figure}

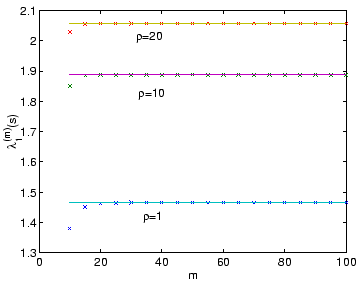
Let us prove that the sequence of largest eigenvalues, $\{\lambda_1^{(m)}(s)\}$, is convergent for $\rho $ fixed. We do this by proving that the sequence is bounded and increasing. Let

\begin{displaymath} D_m=\mathrm{diag}\left(1,1,1,1,1,\frac{1}{\rho}, \frac{1}{2\... ...}, \frac{1}{3\, \rho}, \cdots, \frac{1}{(n-5)\, \rho}\right), \end{displaymath}

and set

\begin{displaymath} \textbf{H}_{m}^{\dagger}(s)= D_m^{-1} \textbf{H}_{m} D_m. \end{displaymath}

The first row of $\textbf{H}_{m}^{\dagger}(s)$ is

\begin{displaymath} (0,0,0,0,0,1,1,1,\cdots,1), \end{displaymath}

the first sub-diagonal is

\begin{displaymath} \left(1,1,1,1,\rho,2,\frac{3}{2},\frac{4}{3},\frac{5}{4}, \cdots, \frac{m-5}{m-4}\right), \end{displaymath}

and the remaining elements of $\textbf{H}_{m}^{\dagger}(s)$ are zero. By applying Geršgorin's Theorem [14, Theorem 7.2.1] columnwise, it follows that all eigenvalues are included in the union of discs which are centered at zero and have radii

\begin{displaymath} r_1=r_2=r_3=r_4=1, \quad r_5=\rho, \quad r_k=\frac{k}{k-1}+1, \quad k=2,3,\cdots,m-5. \end{displaymath}

Therefore,

\begin{displaymath} \vert\lambda_i (\textbf{H}_{m}^{\dagger}(s) )\vert\leq \max\{ \rho,3\}, \quad i=1,2,\cdots m. \end{displaymath}

Since the matrices $\textbf{H}_{m}^{\dagger}(s)$ and $\textbf{H}_m(s)$ have identical eigenvalues the sequence $\{\lambda_1^{(m)}(s)\}$ is bounded. Further, let $P_m(\lambda,s)$ be the characteristic polynomial of $\textbf{H}_m(s)$. Since $\textbf{H}_m(s)$ has the form of the companion matrix, it is easy to see that

\begin{displaymath} P_m(\lambda,s)= \lambda^m-\rho \lambda^{m-6} -2\,\rho\, \lam... ...} - 3\,\rho\, \lambda^{m-8} -\cdots - (m-6)\, \lambda - (m-5). \end{displaymath}

By induction we have

\begin{displaymath} P_{m+1}(\lambda,s)=\lambda\, P_m(\lambda,s)-(m-4). \end{displaymath}

Since $P_{m}(\lambda_1^{(m)}(s),s)=0$, we have

\begin{displaymath} P_{m+1}(\lambda_1^{(m)}(s),s)=\lambda_1^{(m)}(s)\cdot 0 -(m-4)<0. \end{displaymath}

Therefore, $P_{m+1}(\lambda,s)$ has a real zero which is greater than $\lambda _1^{(m)}(s)$. It follows that the sequence $\{\lambda_1^{(m)}(s)\}$ is increasing and, since it is also bounded, convergent. By comparing these results with those of Section 3.2, it is obvious that $\lambda_1^{(m)}(s)\to \lambda_1(s)$. This convergence is very fast, as shown in Figure 3 for $\rho=1,10,20$.

Figure 3: Convergence of $\lambda _1^{(m)}(s)$ (denoted by $\times $) to $\lambda _1(s)$ (solid) for $\rho $=1,10 and 20. Here $m$ is both the number of days (generations) since simulation inception and the order of the matrix. Convergence is rapid in all cases, so that by the twentieth generation of an infestation for practical purposes the finite and infinite values are the same.
\begin{figure}\begin{center} \epsfig{file=eigmax.eps, width=0.5\textwidth}\end{center}\end{figure}

Two questions remain to be answered:

These questions are addressed numerically below.

next up previous
Next: Numerical Tests Up: An Upper Bound for Previous: Determination of Maximum Eigenvalue
James Powell, Ivan Slapnicar and Wopke van der Werf
2002-06-01