

Next: Conclusion
Up: Predicting the Spread of
Previous: Finite Dimensional Case
In numerical simulations
we considered two types of dispersal kernels in (4):
the Gaussian kernel,
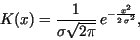 |
(24) |
and the Laplace kernel
 |
(25) |
where  is the mean distance traveled by spores in meters (nominally
set to 1 meter). These two kernels are among the most commonly used for
dispersal studies. The Guassian form describes a process of random
dispersion in the horizontal direction as spores fall from a given height
to the ground; the Laplace kernel describes the net results of a random
horizontal diffusion in time coupled with a constant rate of precipitation of
spores to the ground. Convolution and dispersal were implemented using Fast
Fourier Transforms and the property that the transform of the convolution is
the product of the transforms. In all simulations 4096 grid points were used;
the size of the spatial domain was
is the mean distance traveled by spores in meters (nominally
set to 1 meter). These two kernels are among the most commonly used for
dispersal studies. The Guassian form describes a process of random
dispersion in the horizontal direction as spores fall from a given height
to the ground; the Laplace kernel describes the net results of a random
horizontal diffusion in time coupled with a constant rate of precipitation of
spores to the ground. Convolution and dispersal were implemented using Fast
Fourier Transforms and the property that the transform of the convolution is
the product of the transforms. In all simulations 4096 grid points were used;
the size of the spatial domain was
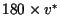 meters, where
meters, where 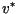 is the
maximum predicted velocity. Given initial conditions starting in the center
of the domain, this gave enough space so that in 60 `days' of simulation a
developing front had 1.5 times as much room to propagate as the maximum speed
linear prediction. Boundary conditions were taken to be periodic.
is the
maximum predicted velocity. Given initial conditions starting in the center
of the domain, this gave enough space so that in 60 `days' of simulation a
developing front had 1.5 times as much room to propagate as the maximum speed
linear prediction. Boundary conditions were taken to be periodic.
Figure 4:
Evolution of the front from initial conditions
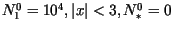 otherwise, in the case of the Laplace kernel (top) and Gauss kernel
(bottom), with nominal
parameters as given in Table 1. The fraction of resource occupied,
otherwise, in the case of the Laplace kernel (top) and Gauss kernel
(bottom), with nominal
parameters as given in Table 1. The fraction of resource occupied,
 , is plotted here. Time slices are ten days apart,
with the evolution of the nonlinear front given by solid lines and the linear
front given by dotted line. Notice that during the last time slice small
round-off errors have grown in advance of the front; these eventually grow and
dominate the solution. The nonlinear solution looks much smoother at this
point because calculation of
, is plotted here. Time slices are ten days apart,
with the evolution of the nonlinear front given by solid lines and the linear
front given by dotted line. Notice that during the last time slice small
round-off errors have grown in advance of the front; these eventually grow and
dominate the solution. The nonlinear solution looks much smoother at this
point because calculation of
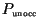 involves summing over age classes,
which smooths the instability.
involves summing over age classes,
which smooths the instability.
 |
Each simulation was performed in the non-linear case using (2),
where
 from (3) was recomputed in each step (each day) using
formula (1), and in the linearized case using (6). The
behavior of
from (3) was recomputed in each step (each day) using
formula (1), and in the linearized case using (6). The
behavior of
 and shape of typical fronts for parameters as in Table
1 and both Laplace and Gaussian kernels is depicted in Figure
4, for both linear and nonlinear growth rates. In both cases,
and shape of typical fronts for parameters as in Table
1 and both Laplace and Gaussian kernels is depicted in Figure
4, for both linear and nonlinear growth rates. In both cases,
 was used to diagnose and depict the location of the front; that is,
to determine the location of the wave of invasion each `day' we would
calculate
was used to diagnose and depict the location of the front; that is,
to determine the location of the wave of invasion each `day' we would
calculate
 (even if it was not used in the dynamics, as in the linear
simulations) and determine the current extent of the invasion by determining
which grid cell contained that point where
(even if it was not used in the dynamics, as in the linear
simulations) and determine the current extent of the invasion by determining
which grid cell contained that point where
 . From the
obtained results we then deduced the speeds of invasion (
. From the
obtained results we then deduced the speeds of invasion (
 and
and
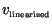 ,
respectively) in both non-linear and linear settings by calculating the
distances propagated over 10 days at the end of the simulation.
,
respectively) in both non-linear and linear settings by calculating the
distances propagated over 10 days at the end of the simulation.
For each simulation we also computed the upper bound of the invasion speed
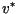 from (10) as follows: we multiplied the composite constant
from (10) as follows: we multiplied the composite constant 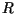 from (5) and the moment generating function
from (5) and the moment generating function  from (8)
to obtain
from (8)
to obtain 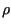 from (18). This
from (18). This 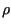 was then inserted into
(23) to obtain
was then inserted into
(23) to obtain 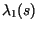 . Finally,
. Finally,  was inserted
into (10), and the minimum over
was inserted
into (10), and the minimum over 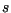 was computed, giving
was computed, giving
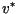 . The speed of invasion
. The speed of invasion  should match the speed obtained by the
simulation in the linearized case. According to (8), the moment
generating function is given by
should match the speed obtained by the
simulation in the linearized case. According to (8), the moment
generating function is given by
for the Gaussian kernel (24), and by
for the Laplace kernel (25).
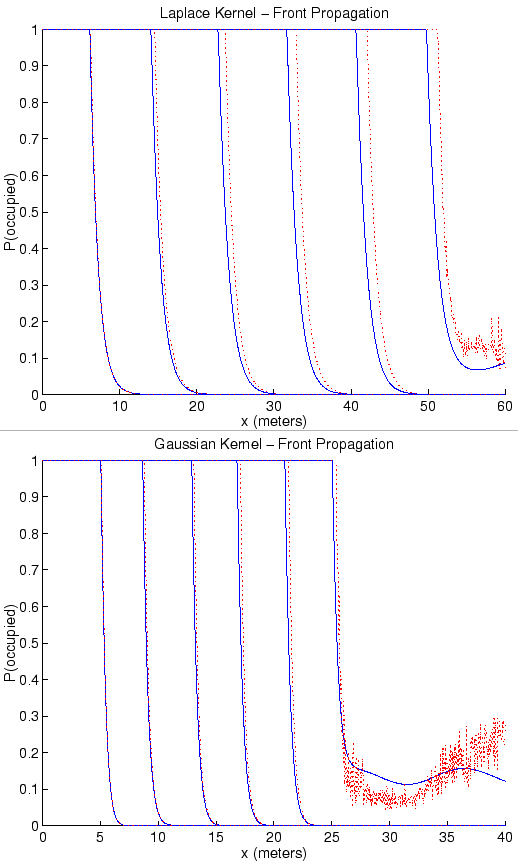
Figure:
Progress of an invasion with mean spore dispersal distances of 1
meter using Gaussian (left) and Laplace (right) kernels. Parameters are set
to nominal values described in Table 1. Invasions were allowed to
progress linearly (unoccupied resource fraction,
 , set always to 1,
dashed lines) and nonlinearly (solid lines). The predicted speeds are
, set always to 1,
dashed lines) and nonlinearly (solid lines). The predicted speeds are
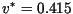 meters/day for the Gaussian kernel and
meters/day for the Gaussian kernel and
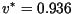 meters/day for the Laplace kernel, which is a small overestimate
of the linear propagation speeds and a larger overestimate of the
nonlinear speeds.
meters/day for the Laplace kernel, which is a small overestimate
of the linear propagation speeds and a larger overestimate of the
nonlinear speeds.
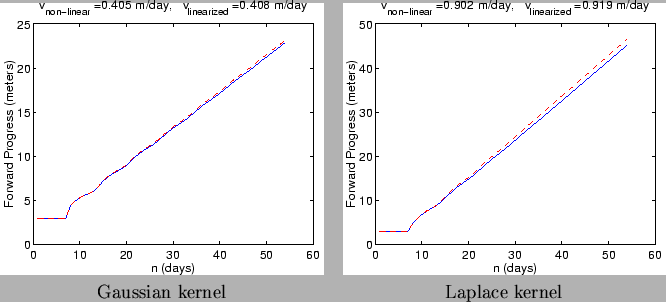 |
Figure 5 shows an example of simulation with nominal values of parameters from
Table 1. For these values, the composite constant  from (5) and
(17) is equal to
from (5) and
(17) is equal to 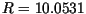 . The simulation was run with Gaussian and
Laplace kernel, respectively, with
. The simulation was run with Gaussian and
Laplace kernel, respectively, with 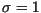 in both cases.
Solid curves show the progress of infection in the non-linear cases, and
dashed curves show the progress in the linearized cases with
in both cases.
Solid curves show the progress of infection in the non-linear cases, and
dashed curves show the progress in the linearized cases with
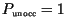 in
(3).
For this example the theoretical speeds are
in
(3).
For this example the theoretical speeds are
 meters/day for the Gaussian kernel and
meters/day for the Gaussian kernel and
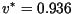 meters/day for the Laplace kernel.
We see that, for both kernels, the speeds obtained by linearization,
meters/day for the Laplace kernel.
We see that, for both kernels, the speeds obtained by linearization,
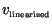 ,
overestimate the speeds of the nonlinear model,
,
overestimate the speeds of the nonlinear model,
 ,
and the theoretical speeds
,
and the theoretical speeds  slightly overestimate
slightly overestimate
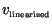 .
This is quite interesting, as the dynamic perspective on front propagation
would suggest that
.
This is quite interesting, as the dynamic perspective on front propagation
would suggest that 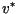 should be the asymptotic speed for both linear and
nonlinear fronts, and simulation result with fixed-size Leslie matrices
indicate rapid convergence to the predicted minimal wave speed (see, for
example, Neubert and Caswell [15]).
should be the asymptotic speed for both linear and
nonlinear fronts, and simulation result with fixed-size Leslie matrices
indicate rapid convergence to the predicted minimal wave speed (see, for
example, Neubert and Caswell [15]).
To more completely investigate the comparative behavior of
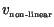 versus
versus 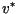 and
and
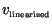 versus
versus 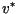 ,
we performed a series of simulations with different values of parameters from
Table 1 in a randomized factorial design. The first three parameters
(
,
we performed a series of simulations with different values of parameters from
Table 1 in a randomized factorial design. The first three parameters
(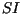 ,
,  and
and 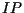 ) were kept at their
nominal values, while the remaining five parameters were chosen as follows:
) were kept at their
nominal values, while the remaining five parameters were chosen as follows:
This gives the total of 432 simulations for each kernel.
In these simulations, the composite constant 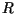 attained values in the interval
attained values in the interval
![$R\in[0.3534,15.7080]$](img179.gif) , and the theoretical bound for invasion speed
, and the theoretical bound for invasion speed
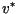 attained values
attained values
![$v^*\in[0.1198,0.8755]$](img180.gif) for the Gaussian kernel and
for the Gaussian kernel and
![$v^*\in[0.2376,2.0106]$](img181.gif) for the Laplace kernel.
The results of simulations are summarized in Figure 6.
for the Laplace kernel.
The results of simulations are summarized in Figure 6.
Figure 6:
Comparison of predicted and observed speeds for waves of invasion
with and without density dependent growth restrictions for both Laplace and
Gaussian dispersal kernels. Parameters are chosen in a random factorial
design described in the text, with variation centered on the nominal values
described in Table 1. Observed linear and nonlinear speeds are marked with
` ' and `*' respectively. The solid line is the line
' and `*' respectively. The solid line is the line
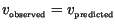 , indicating perfect agreement. Results indicate a consistent
overprediction of observation by prediction, with a greater degree of error
for nonlinear as compared to linear propagation.
, indicating perfect agreement. Results indicate a consistent
overprediction of observation by prediction, with a greater degree of error
for nonlinear as compared to linear propagation.
 |
The size of the error between observation and prediction depicted in Figure
6 reflects what appears to be a consistent overprediction of
observed linear and nonlinear speeds, with the degree of overprediction being
approximately double for nonlinear speeds as compared to linear speeds.
From the minimal speed perspective this is not so awful; after all, 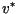 is
an upper bound, but only in relatively rare cases has it been proven to be the
asymptotic speed of fronts. On the other hand, the
agreement between prediction and observation is generally superb (see, for
example, Neubert et al. [15,16])- why should
it be less so in this case? And what of the dynamic argument, which suggests
that fronts should accelerate to
is
an upper bound, but only in relatively rare cases has it been proven to be the
asymptotic speed of fronts. On the other hand, the
agreement between prediction and observation is generally superb (see, for
example, Neubert et al. [15,16])- why should
it be less so in this case? And what of the dynamic argument, which suggests
that fronts should accelerate to  ?
?
The explanation for the degree of observation lies in three interrelated
effects in our simulation. In the first place, the net daily per-capita
growth rate for the number of
fungal lesions was never less than 1.5 in our simulations, and was often as
large as 10, reflecting the extremely invasive nature of this pathogen. As a
consequence, simulations were difficult to run for long periods of time; at
some point small round-off errors in the neighborhood of zero would start to
grow geometrically. So, in practice we were unable to maintain simulations
much beyond 50 iterations, and running longer simulations to allow for greater
convergence was impossible both because of the extreme instability of the zero
population state as well as the size of the transition matrices (which are as
large as
the number of days) at each spatial location.
Confounded with this effect are two convergence effects, each
contributing to the overprediction. In the first place there is the
convergence to the stable travelling population distribution, which is
described by the first neglected terms in the power method. Thus, when
considering the evolution of a front from compact initial data, the asymptotic
problem should read
Here
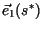 can be interpreted as the asymptotic stable population
distribution selected by the wave of invasion, while
can be interpreted as the asymptotic stable population
distribution selected by the wave of invasion, while
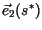 is the
age structure of the `ringing' which occurs as population distributions
converge to the stable distribution along a front, and the ratio of the
largest and second-largest magnitude eigenvalues is the rate of convergence.
This is asymptotically negligible, but for finite duration simulations (like
those we are forced to run by the extreme instability of the system) we may
expect an error in estimating front speeds proportional to
is the
age structure of the `ringing' which occurs as population distributions
converge to the stable distribution along a front, and the ratio of the
largest and second-largest magnitude eigenvalues is the rate of convergence.
This is asymptotically negligible, but for finite duration simulations (like
those we are forced to run by the extreme instability of the system) we may
expect an error in estimating front speeds proportional to
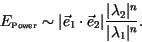 |
(26) |
The second convergence effect is the natural acceleration of the front to the
asymptotic front speed described by (16). Predicted by the
steepest descent methodology, this can be viewed as the convergence of the
spatial shape of the front to the asymptotic exponential shape which is a
translate of  . The speed convergence error predicted by the
steepest descents approach is (from 16)
. The speed convergence error predicted by the
steepest descents approach is (from 16)
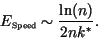 |
(27) |
While
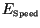 tends to zero as
tends to zero as  tends to infinity, the
convergence is slow, and again the constraint that we were unable to
simulate for more than several tens of iterations means that this error can
not be neglected.
tends to infinity, the
convergence is slow, and again the constraint that we were unable to
simulate for more than several tens of iterations means that this error can
not be neglected.
To investigate how these errors relate to observed errors in our simulation we
ran each of the factorially crossed parameter studies for as long as possible,
diagnosing the onset of overwhelming instability by the inevitable sudden jump
in the rate of progress of the front. In each simulation the day at which the
simulation `broke' was diagnosed by and recorded as  . During each
simulation the forward progress (
. During each
simulation the forward progress (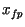 ) of the front was diagnosed as
described above. Observed speeds were then diagnosed by
) of the front was diagnosed as
described above. Observed speeds were then diagnosed by
Simultaneously, the largest two eigenvalues of the finite transition matrix,
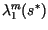 and
and
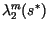 , were calculated, with
, were calculated, with  evaluated at the center of the speed calculation interval,
evaluated at the center of the speed calculation interval, 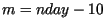 . With
this information we could determine the size of the two error components,
. With
this information we could determine the size of the two error components,
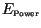 and
and
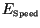 . These errors are
compared to the observed relative speed error,
. These errors are
compared to the observed relative speed error,
in Figures 7 and 8.
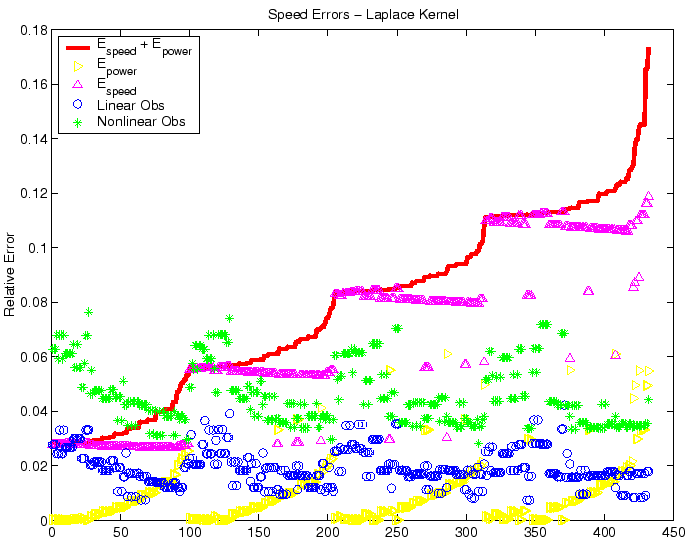
Figure 7:
Raw comparison of observed relative speed errors in the nonlinear
(`*') and linear (` ') cases for the Gaussian kernel, with randomized
choices of parametric data, centered on the nominal values in Table 1. The
asymptotic error size due to age structure convergence,
') cases for the Gaussian kernel, with randomized
choices of parametric data, centered on the nominal values in Table 1. The
asymptotic error size due to age structure convergence,
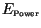 , is plotted as `
, is plotted as `
 ', while asymptotic error size due
to speed convergence,
', while asymptotic error size due
to speed convergence,
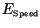 , appears as `
, appears as ` '.
The total error size,
'.
The total error size,
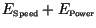 is the solid line; results were sorted in terms of increasing
total error. The horizontal axis is the identifying index of the simulation
and has no units. Given that the actual error
relates by an order one factor to the error sizes depicted here, both the
linear and nonlinear front speeds are well within acceptable error bounds.
is the solid line; results were sorted in terms of increasing
total error. The horizontal axis is the identifying index of the simulation
and has no units. Given that the actual error
relates by an order one factor to the error sizes depicted here, both the
linear and nonlinear front speeds are well within acceptable error bounds.
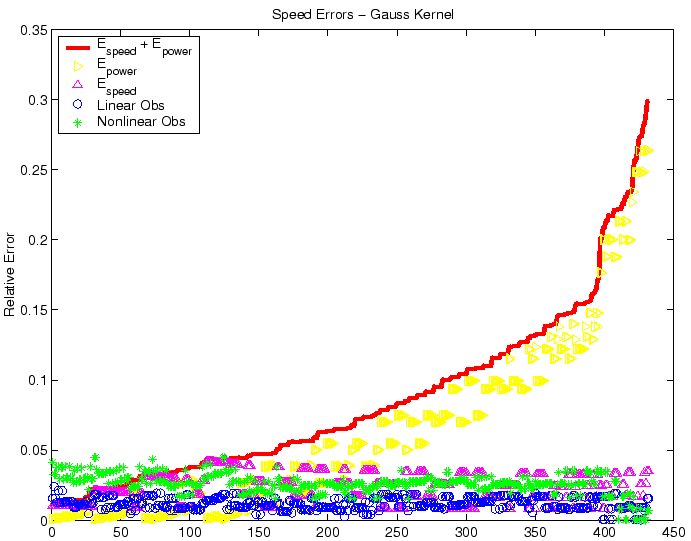 |
Figure 8:
Raw comparison of observed relative speed errors in the nonlinear
(`*') and linear (` ') cases for the Laplace kernel, with randomized
choices of parametric data, centered on the nominal values in Table 1. The
asymptotic error size due to age structure convergence,
') cases for the Laplace kernel, with randomized
choices of parametric data, centered on the nominal values in Table 1. The
asymptotic error size due to age structure convergence,
 , is plotted as `
, is plotted as `
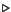 ', while asymptotic error size due
to speed convergence,
', while asymptotic error size due
to speed convergence,
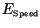 , appears as `
, appears as `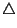 '.
The total error size,
'.
The total error size,
 is the solid line; results were sorted in terms of increasing
total error. The horizontal axis is the identifying index of the simulation
and has no units. Given that the actual error
relates by an order one factor to the error sizes depicted here, both the
linear and nonlinear front speeds are well within acceptable error bounds.
is the solid line; results were sorted in terms of increasing
total error. The horizontal axis is the identifying index of the simulation
and has no units. Given that the actual error
relates by an order one factor to the error sizes depicted here, both the
linear and nonlinear front speeds are well within acceptable error bounds.
 |


Next: Conclusion
Up: Predicting the Spread of
Previous: Finite Dimensional Case
James Powell, Ivan Slapnicar and Wopke van der Werf
2002-06-01

![]() from (3) was recomputed in each step (each day) using
formula (1), and in the linearized case using (6). The
behavior of
from (3) was recomputed in each step (each day) using
formula (1), and in the linearized case using (6). The
behavior of
![]() and shape of typical fronts for parameters as in Table
1 and both Laplace and Gaussian kernels is depicted in Figure
4, for both linear and nonlinear growth rates. In both cases,
and shape of typical fronts for parameters as in Table
1 and both Laplace and Gaussian kernels is depicted in Figure
4, for both linear and nonlinear growth rates. In both cases,
![]() was used to diagnose and depict the location of the front; that is,
to determine the location of the wave of invasion each `day' we would
calculate
was used to diagnose and depict the location of the front; that is,
to determine the location of the wave of invasion each `day' we would
calculate
![]() (even if it was not used in the dynamics, as in the linear
simulations) and determine the current extent of the invasion by determining
which grid cell contained that point where
(even if it was not used in the dynamics, as in the linear
simulations) and determine the current extent of the invasion by determining
which grid cell contained that point where
![]() . From the
obtained results we then deduced the speeds of invasion (
. From the
obtained results we then deduced the speeds of invasion (
![]() and
and
![]() ,
respectively) in both non-linear and linear settings by calculating the
distances propagated over 10 days at the end of the simulation.
,
respectively) in both non-linear and linear settings by calculating the
distances propagated over 10 days at the end of the simulation.
![]() from (10) as follows: we multiplied the composite constant
from (10) as follows: we multiplied the composite constant ![]() from (5) and the moment generating function
from (5) and the moment generating function ![]() from (8)
to obtain
from (8)
to obtain ![]() from (18). This
from (18). This ![]() was then inserted into
(23) to obtain
was then inserted into
(23) to obtain ![]() . Finally,
. Finally, ![]() was inserted
into (10), and the minimum over
was inserted
into (10), and the minimum over ![]() was computed, giving
was computed, giving
![]() . The speed of invasion
. The speed of invasion ![]() should match the speed obtained by the
simulation in the linearized case. According to (8), the moment
generating function is given by
should match the speed obtained by the
simulation in the linearized case. According to (8), the moment
generating function is given by

![]() from (5) and
(17) is equal to
from (5) and
(17) is equal to ![]() . The simulation was run with Gaussian and
Laplace kernel, respectively, with
. The simulation was run with Gaussian and
Laplace kernel, respectively, with ![]() in both cases.
Solid curves show the progress of infection in the non-linear cases, and
dashed curves show the progress in the linearized cases with
in both cases.
Solid curves show the progress of infection in the non-linear cases, and
dashed curves show the progress in the linearized cases with
![]() in
(3).
For this example the theoretical speeds are
in
(3).
For this example the theoretical speeds are
![]() meters/day for the Gaussian kernel and
meters/day for the Gaussian kernel and
![]() meters/day for the Laplace kernel.
We see that, for both kernels, the speeds obtained by linearization,
meters/day for the Laplace kernel.
We see that, for both kernels, the speeds obtained by linearization,
![]() ,
overestimate the speeds of the nonlinear model,
,
overestimate the speeds of the nonlinear model,
![]() ,
and the theoretical speeds
,
and the theoretical speeds ![]() slightly overestimate
slightly overestimate
![]() .
This is quite interesting, as the dynamic perspective on front propagation
would suggest that
.
This is quite interesting, as the dynamic perspective on front propagation
would suggest that ![]() should be the asymptotic speed for both linear and
nonlinear fronts, and simulation result with fixed-size Leslie matrices
indicate rapid convergence to the predicted minimal wave speed (see, for
example, Neubert and Caswell [15]).
should be the asymptotic speed for both linear and
nonlinear fronts, and simulation result with fixed-size Leslie matrices
indicate rapid convergence to the predicted minimal wave speed (see, for
example, Neubert and Caswell [15]).
![]() versus
versus ![]() and
and
![]() versus
versus ![]() ,
we performed a series of simulations with different values of parameters from
Table 1 in a randomized factorial design. The first three parameters
(
,
we performed a series of simulations with different values of parameters from
Table 1 in a randomized factorial design. The first three parameters
(![]() ,
, ![]() and
and ![]() ) were kept at their
nominal values, while the remaining five parameters were chosen as follows:
) were kept at their
nominal values, while the remaining five parameters were chosen as follows:

![]() is
an upper bound, but only in relatively rare cases has it been proven to be the
asymptotic speed of fronts. On the other hand, the
agreement between prediction and observation is generally superb (see, for
example, Neubert et al. [15,16])- why should
it be less so in this case? And what of the dynamic argument, which suggests
that fronts should accelerate to
is
an upper bound, but only in relatively rare cases has it been proven to be the
asymptotic speed of fronts. On the other hand, the
agreement between prediction and observation is generally superb (see, for
example, Neubert et al. [15,16])- why should
it be less so in this case? And what of the dynamic argument, which suggests
that fronts should accelerate to ![]() ?
?
![\begin{eqnarray*}
e^{ns^*v^*} \ \vec{w} =
\textbf{H}^n (s^*) \ \vec{w} &=& a_1(...
...rac{\lambda_2^n}{\lambda_1^n} \vec{e}_2(s^*) + \cdots
\right].
\end{eqnarray*}](img184.gif)
![]() . The speed convergence error predicted by the
steepest descents approach is (from 16)
. The speed convergence error predicted by the
steepest descents approach is (from 16)
![]() . During each
simulation the forward progress (
. During each
simulation the forward progress (![]() ) of the front was diagnosed as
described above. Observed speeds were then diagnosed by
) of the front was diagnosed as
described above. Observed speeds were then diagnosed by

