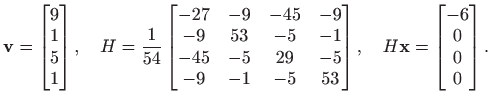U ovom i sljedećem poglavlju opisat ćemo detalje QR algoritma.
Neka je zadan ![]() -dimenzionalni vektor
-dimenzionalni vektor
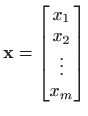
i neka je
njegov QR rastav. Tada je zbog svojstva (6.3)
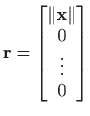 ili
ili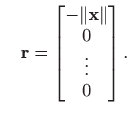
Nalaženje matrice
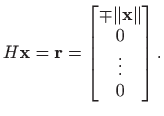
Ortogonalnosti i simetričnosti matrice
pa smo dobili QR rastav vektora