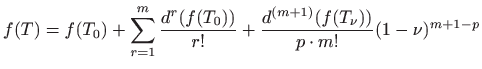☰
matematika2
Određeni integral
Višestruki integrali
Funkcije više varijabla
- 1.
- Definirajte
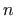 -dimenzionalni prostor
-dimenzionalni prostor
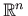 . Na koje sve
načine možemo zadati funkciju
. Na koje sve
načine možemo zadati funkciju
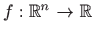 ?
Što su nivo-plohe?
?
Što su nivo-plohe?
![[*]](../icons.gif/crossref.gif)
- 2.
- Kako definiramo udaljenost? Što je otvorena kugla
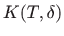 ?
?
![[*]](../icons.gif/crossref.gif)
- 3.
- Definicija limesa funkcije više varijabli:
![[*]](../icons.gif/crossref.gif)
ako
tako da
Kako možemo limes definirati pomoću nizova?
![[*]](../icons.gif/crossref.gif)
- 4.
- Definirajte neprekidnost funkcije više varijabla.
![[*]](../icons.gif/crossref.gif)
- 5.
- Neprekidna funkcija poprima na zatvorenom skupu svoj maksimum i
minimum.
![[*]](../icons.gif/crossref.gif)
- 6.
- Navedite formule za standardne plohe drugog reda (kugla, elipsoid,
stožac, razni paraboloidi, razni cilindri).
![[*]](../icons.gif/crossref.gif)
- 7.
- Definicija parcijalnih derivacija.
![[*]](../icons.gif/crossref.gif)
![[*]](../icons.gif/crossref.gif)
- 8.
- Schwartzov teorem.
![[*]](../icons.gif/crossref.gif)
- 9.
- Definicija totalnog diferencijala.
![[*]](../icons.gif/crossref.gif)
![[*]](../icons.gif/crossref.gif)
- 10.
- Je li svaka neprekidno derivabilna funkcija i diferencijabilna?
![[*]](../icons.gif/crossref.gif)
- 11.
- Definirajte tangencijalnu ravninu i normalu na plohu.
![[*]](../icons.gif/crossref.gif)
- 12.
- Parcijalno deriviranje složene funkcije (kompozicije funkcija).
![[*]](../icons.gif/crossref.gif)
- 13.
- Totalni diferencijal višeg reda.
![[*]](../icons.gif/crossref.gif)
- 14.
- Taylorova formula za funkcije više varijabla:
![[*]](../icons.gif/crossref.gif)
Razvijte funkciju 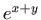 u Taylorov red u okolini točke
u Taylorov red u okolini točke 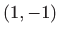 .
.
- 15.
- Kako definiramo lokalne ekstreme funkcije više varijabla?
![[*]](../icons.gif/crossref.gif)
- 16.
- Kako glasi nuždan uvjet ekstrema funkcije više varijabla?
![[*]](../icons.gif/crossref.gif)
- 17.
- Kako glasi dovoljan uvjet ekstrema pomoću totalnog diferencijala?
![[*]](../icons.gif/crossref.gif)
- 18.
- Kako glasi dovoljan uvjet ekstrema pomoću pod-determinanti matrice drugih
parcijalnih derivacija? Dajte primjere.
![[*]](../icons.gif/crossref.gif)
- 19.
- Što su implicitno zadane funkcije? Izrecite Teorem o implicitnoj
funkciji i navedite primjere.
![[*]](../icons.gif/crossref.gif)
- 20.
- Izvedite nužne uvjete za uvjetni ekstrem funkcije dvije
varijable. Dajte primjere.
![[*]](../icons.gif/crossref.gif)
Određeni integral
Višestruki integrali