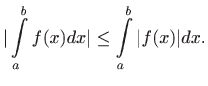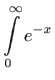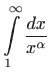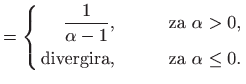☰
matematika2
Neodređeni integral
Funkcije više varijabla
Određeni integral
- 1.
- Definirajte određeni (Riemannov) integral.
![[*]](../icons.gif/crossref.gif)
- 2.
- Objasnite osnovna svojstva određenog integrala:
![[*]](../icons.gif/crossref.gif)
- a)
- ako je
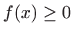 za svaki
za svaki
![$ x\in
[a,b]$](img43.gif) , tada
, tada
daje površinu između 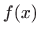 i
i 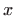 -osi od
-osi od 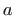 do
do 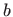 ,
,
- b)
- vrijedi
- c)
- vrijedi
- d)
- vrijedi
- 3.
- Što je određeni, a što neodređeni integral?
![[*]](../icons.gif/crossref.gif)
- 4.
- Dokažite Newton-Leibnitzovu formulu.
![[*]](../icons.gif/crossref.gif)
- 5.
- Ako je funkcija
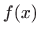 integrabilna na intervalu
integrabilna na intervalu ![$ [a,b]$](img51.gif) ,
tada je jedna primitivna
funkcija dana s
,
tada je jedna primitivna
funkcija dana s
Dokažite!
![[*]](../icons.gif/crossref.gif)
- 6.
- Dokažite teorem srednje vrijednosti za određeni
integral: ako je
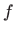 neprekidna na
neprekidna na ![$ [a,b]$](img51.gif) , onda postoji
, onda postoji ![$ c\in[a,b]$](img54.gif) za koji je
za koji je
![[*]](../icons.gif/crossref.gif)
Koja je grafička interpretacija tog teorema?
![[*]](../icons.gif/crossref.gif)
- 7.
- Dokažite
- a)
- monotonost:
![[*]](../icons.gif/crossref.gif)
- b)
- nejednakost trokuta:
![[*]](../icons.gif/crossref.gif)
- 8.
-
![[*]](../icons.gif/crossref.gif) Što je nepravi integral? Dokažite:
Što je nepravi integral? Dokažite:
![[*]](../icons.gif/crossref.gif)
- 9.
- Opišite kriterije konvergencije za nepravi integral
(majoranta, minoranta, apsolutna konvergencija).
![[*]](../icons.gif/crossref.gif)
- 10.
- Kako računamo površinu ravninskih likova? Izvedite element površine
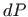 u
Kartezijevim koordinatama,
u
Kartezijevim koordinatama,
![[*]](../icons.gif/crossref.gif)
i polarnim koordinatama,
![[*]](../icons.gif/crossref.gif)
![[*]](../icons.gif/crossref.gif) Izvedite
Izvedite 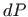 za parametarski zadane krivulje. Dajte primjere.
za parametarski zadane krivulje. Dajte primjere.
![[*]](../icons.gif/crossref.gif)
![[*]](../icons.gif/crossref.gif)
![[*]](../icons.gif/crossref.gif)
![[*]](../icons.gif/crossref.gif)
![[*]](../icons.gif/crossref.gif)
![[*]](../icons.gif/crossref.gif)
![[*]](../icons.gif/crossref.gif)
- 11.
-
![[*]](../icons.gif/crossref.gif) Kako računamo duljinu luka ravninske krivulje? Izvedite
Kako računamo duljinu luka ravninske krivulje? Izvedite 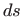 u
Kartezijevim koordinatama,
u
Kartezijevim koordinatama,
i polarnim koordinatama,
![[*]](../icons.gif/crossref.gif)
![[*]](../icons.gif/crossref.gif) Izvedite
Izvedite 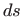 za parametarski zadane krivulje. Dajte primjere.
za parametarski zadane krivulje. Dajte primjere.
![[*]](../icons.gif/crossref.gif)
![[*]](../icons.gif/crossref.gif)
![[*]](../icons.gif/crossref.gif)
- 12.
- Slično pitanje za obujam rotacionih tijela.
![[*]](../icons.gif/crossref.gif)
- 13.
- Slično pitanje za oplošje rotacionih ploha (komplanacija).
![[*]](../icons.gif/crossref.gif)
- 14.
- Objasnite postupak numeričkog integriranja
![[*]](../icons.gif/crossref.gif) (
(
![[*]](../icons.gif/crossref.gif) trapezna formula,
trapezna formula,
![[*]](../icons.gif/crossref.gif) Simpsonova
formula,
Simpsonova
formula,
![[*]](../icons.gif/crossref.gif) Richardsonova ekstrapolacija)?
Richardsonova ekstrapolacija)?
Neodređeni integral
Funkcije više varijabla
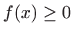 za svaki
za svaki
![$ x\in
[a,b]$](img43.gif) , tada
, tada
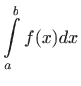
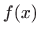 i
i 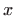 -osi od
-osi od 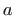 do
do 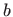 ,
,
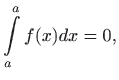
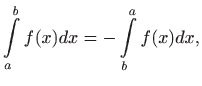
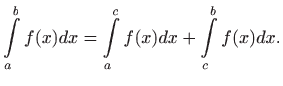
![$\displaystyle F(x)=\int\limits _a^x f(x)dx, \quad x\in [a,b], \quad F(a)=0.
$](img52.gif)
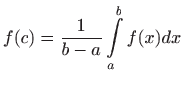
![[*]](../icons.gif/crossref.gif)
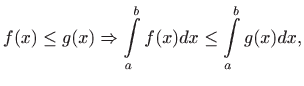
![[*]](../icons.gif/crossref.gif)