Slično kao kod redova brojeva
(vidi
![]()
![]()
![]() M1, teorem 6.10 i teorem 6.11)
i kod nepravog integrala možemo zaključiti
je li konvergira bez računanja samog integrala.
M1, teorem 6.10 i teorem 6.11)
i kod nepravog integrala možemo zaključiti
je li konvergira bez računanja samog integrala.
Poredbeni kriterij
glasi: ako je
![]() za svaki
za svaki
![]() , pri čemu su
, pri čemu su ![]() i
i ![]() granice nepravog
integrala, onda
konvergencija integrala
granice nepravog
integrala, onda
konvergencija integrala
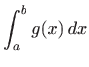 povlači konvergenciju
integrala
povlači konvergenciju
integrala
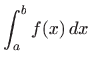 , a
divergencija integrala
, a
divergencija integrala
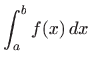 povlači divergenciju
integrala
povlači divergenciju
integrala
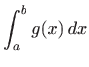 .
.
Teorem o apsolutnoj
konvergenciji
glasi:
konvergencija integrala
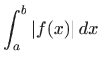 povlači konvergenciju
integrala
povlači konvergenciju
integrala
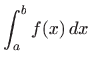 .
.
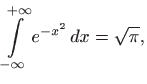
koji ima važnu primjenu u teoriji vjerojatnosti, nije elementarno rješiv. Međutim, koristeći poredbeni kriterij lako vidimo da taj integral konvergira. Kako je podintegralna funkcija parna, očito vrijedi (slika 2.10)
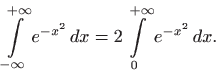
Iz slike 2.10, činjenica da za
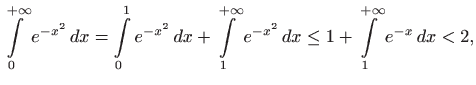
pa promatrani integral konvergira.
Kao ilustraciju apsolutne konvergencije promotrimo integral (vidi sliku 2.11)
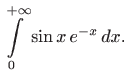
Kako za
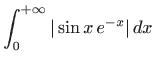 konvergira. No, onda i zadani integral konvergira po teoremu o
apsolutnoj konvergenciji.
konvergira. No, onda i zadani integral konvergira po teoremu o
apsolutnoj konvergenciji.