☰ matematika2

Populacijska i logistička jednadžba DIFERENCIJALNE JEDNADŽBE Polje smjerova

Jednadžbe sa separiranim varijablama

Diferencijalna jednadžba prvog reda je separabilna (kažemo i da se radi o jednadžbi sa separiranim varijablama) ako je možemo zapisati u obliku.

$\displaystyle f(x) dx=g(y) dy.$

Onda je

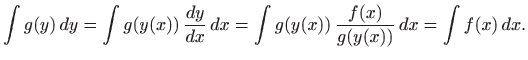
$\displaystyle \int g(y) dy=\int g(y(x)) \frac{dy}{dx} dx =\int g(y(x)) \frac{f(x)}{g(y(x))} dx =\int f(x) dx.$

U literaturi se često navodi i oblik:

$\displaystyle P(x) dx+Q(y) dy=0.$

Sve jednadžbe prvog reda koje smo rješavali u prethodnim poglavljima su separabilne. Navedimo još nekoliko primjera.

Primjer 5.7 Za jednadžbu

$\displaystyle \frac{dy}{dx}=\frac{x^2}{2y+\sin y}$

vrijedi

$\displaystyle (2y + \sin y) dy= x^2 dx$

pa je implicitno rješenje jednadžbe dano s

$\displaystyle y^2 -\cos y = \frac{x^3}{3} + C.$

Ako je još zadan i početni uvjet $y(1)=\pi$ , onda je

$\displaystyle C=\pi^2 +\frac{2}{3}.$

Primjer 5.8 Newtonov zakon hlađenja kaže da je promjena temperature objekta proporcionalna razlici temperature objekta

i temperature okoline (ambijenta) $T_{\mathrm{amb}}$ . Ovaj zakon je dobra aproksimacija procesa hlađenja u standardnim uvjetima. Matematička formulacija glasi

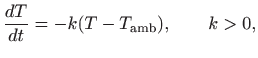
$\displaystyle \frac{dT}{dt}=-k(T-T_{\mathrm{amb}}), \qquad k> 0,$

gdje je

koeficijent hlađenja (koji ovisi, na primjer, o izolacijskim svojstvima posude). Rješenje problema hlađenja je:

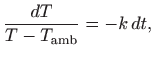	$\displaystyle \frac{dT}{T-T_{\mathrm{amb}}}=-k dt,$
	$\displaystyle \ln\vert T-T_{\mathrm{amb}}\vert=-kt+C,$
	$\displaystyle \vert T-T_{\mathrm{amb}}\vert=e^{-kt}e^C,$
	$\displaystyle T-T_{\mathrm{amb}}=A e^{-kt}.$

Ako je zadana početna temperatura

, onda je $T_0=T(0)=T_{\mathrm{amb}}+A$ pa je konačno

$\displaystyle T(t)=e^{-kt}(T_0-T_{\mathrm{amb}})+T_{\mathrm{amb}}.$

Zadatak 5.2

a)

U jednu veliku šalicu kave temperature $90^\circ \mathrm{C}$ ulijemo mlijeko sobne temperature od $22^\circ \mathrm{C}$ odmah, a u drugu nakon 5 minuta. Koja će kava biti toplija nakon 8 minuta? Što se događa ako ulijemo mlijeko iz frižidera temperature $4^\circ \mathrm{C}$ ? Napomena: ako je količina kave

i temperatura kave

te ako je količina mlijeka

i temperatura mlijeka

, onda je temperatura smjese

jednaka

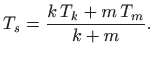
$\displaystyle T_s =\frac{k T_k+m T_m}{k+m}.$

b)

U hotelskoj sobi temperature $20^\circ \mathrm{C}$ policija je u ponoć otkrila tijelo žrtve. Temperatura tijela bila je $26^\circ \mathrm{C}$ . Dva sata kasnije temperatura tijela bila je $24^\circ \mathrm{C}$ . Kada se otprilike dogodio zločin?

Funkcija je homogena stupnja homogenosti ako je

$\displaystyle f(\lambda x,\lambda y) = \lambda^k f(x,y).$

Diferencijalna jednadžba oblika

$\displaystyle P(x,y) dx+Q(x,y) dy=0$

homogena je ako su

homogene funkcije istog stupnja. Zamjenom varijabli

homogena jednadžba prelazi u jednadžbu sa separiranim varijablama.

Primjer 5.9 Riješimo diferencijalnu jednadžbu

$\displaystyle y'=\frac{xy}{x^2-y^2}.$

Kako je

$\displaystyle \frac{(\lambda x)(\lambda y)}{(\lambda x)^2-(\lambda y)^2}=\frac{\lambda^2 xy}{\lambda^2(x^2-y^2)}= \frac{xy}{x^2-y^2},$

zadana jednadžba je homogena. Uvrštavanje

$\displaystyle y=zx,\qquad y'=z'x+z$

uz $x\neq 0$ daje

$\displaystyle z'x+z=\frac{x^2 z}{x^2-x^2z^2}=\frac{z}{1-z^2}.$

Sada imamo

	$\displaystyle \frac{1-z^2}{z^3} dz= \frac{1}{x} dx,$
	$\displaystyle -\frac{1}{2z^2}-\ln z = \ln x + \ln C,$

gdje smo radi jednostavnosti pretpostavili da je

. Sada je

	$\displaystyle -\frac{1}{2z^2}=\ln(z x C),$
	$\displaystyle z x C=e^{-1/(2z^2)},$
	$\displaystyle \frac{y}{x} x C = e^{-x^2/(2y^2)},$

i, konačno,

$\displaystyle y=\frac{1}{C} e^{-x^2/(2y^2)}.$

Zadatak 5.3 Riješite diferencijalne jednadžbe:

a): $\left(y'-\displaystyle \frac{y}{x}\right)\mathop{\mathrm{arctg}}\nolimits \displaystyle \frac{y}{x}=0$ uz ,
b): ,
c): $y'= \displaystyle \frac{x \sqrt{1+x^2}}{y e^y}$ .

Zadatak 5.4 Nađite jednadžbu krivulje koja prolazi točkom

, a ima svojstvo da joj je nagib u točki

jednak

Populacijska i logistička jednadžba DIFERENCIJALNE JEDNADŽBE Polje smjerova