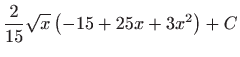 .
.
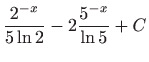 .
.
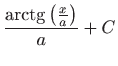 .
.
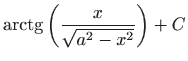 .
.
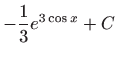 .
.
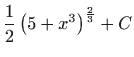 .
.
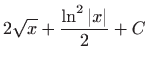 .
.
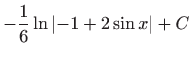 .
.
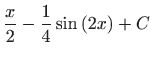 .
.
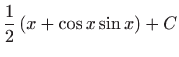 .
.
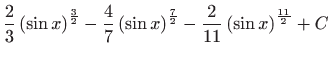 .
.
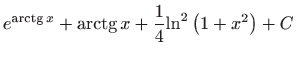 .
.
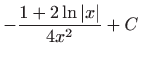 .
.
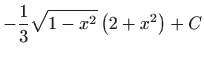 .
.
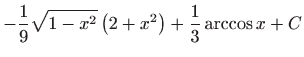 .
.
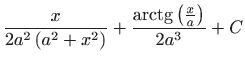 .
.
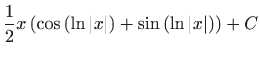 .
.
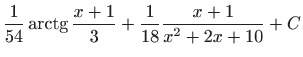 .
.
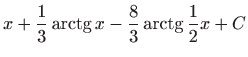 .
.
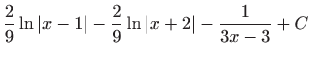 .
.
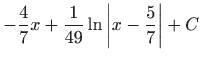 .
.
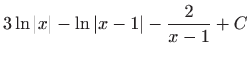 .
.
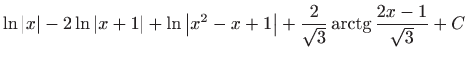 .
.
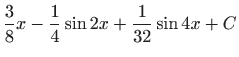 .
.
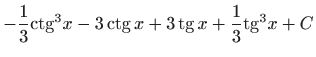 .
.
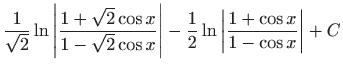 .
.
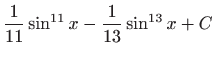 .
.
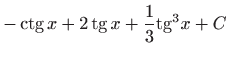 .
.
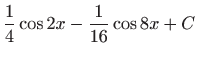 .
.
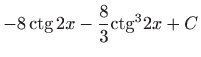 .
.
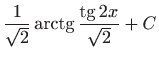 .
.
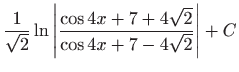 .
.
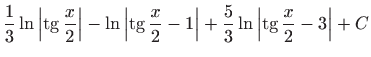 .
.
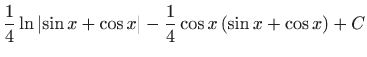 .
.
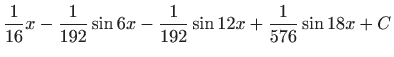 .
.
![$ \displaystyle \frac{3}{2}\sqrt[3] {x^2}+\mathop{\mathrm{arctg}}\nolimits \sqrt[6] x
+C$](img456.gif) .
.
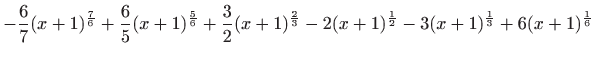
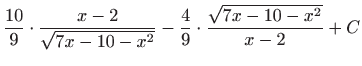 .
.
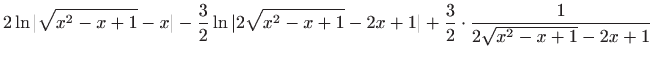
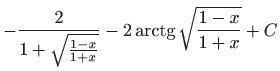 .
.
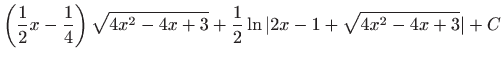 .
.
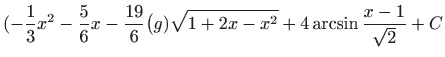 .
.
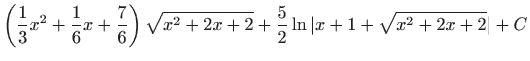 .
.
![$ \displaystyle -\frac{1}{2(\sqrt[4]
x+1)^8}+\frac{4}{9(\sqrt[4] x+1)^9}+C$](img467.gif) .
.
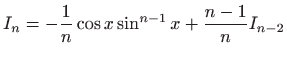 ,
, 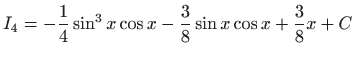 .
.
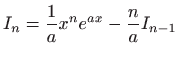 .
.
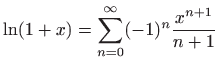 ,
,
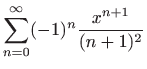 ,
,
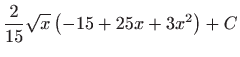 .
.
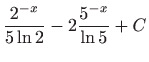 .
.
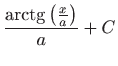 .
.
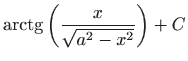 .
.
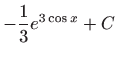 .
.
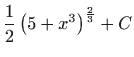 .
.
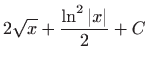 .
.
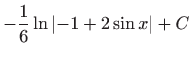 .
.
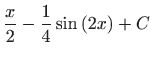 .
.
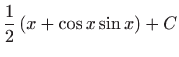 .
.
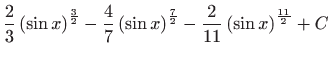 .
.
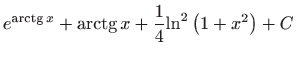 .
.
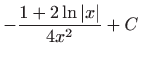 .
.
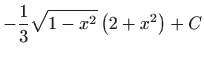 .
.
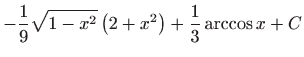 .
.
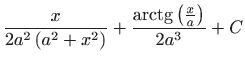 .
.
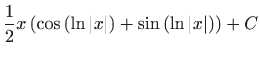 .
.
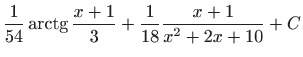 .
.
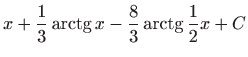 .
.
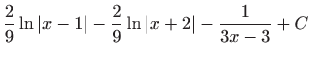 .
.
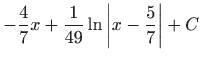 .
.
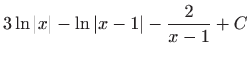 .
.
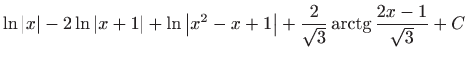 .
.
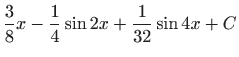 .
.
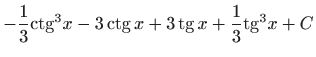 .
.
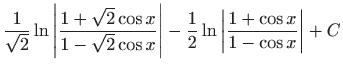 .
.
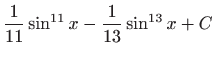 .
.
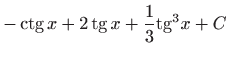 .
.
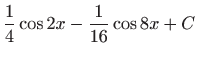 .
.
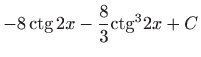 .
.
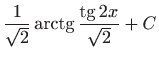 .
.
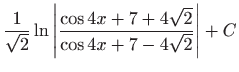 .
.
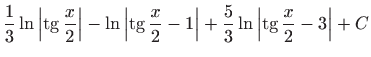 .
.
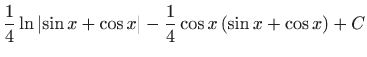 .
.
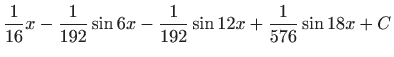 .
.
![$ \displaystyle \frac{3}{2}\sqrt[3] {x^2}+\mathop{\mathrm{arctg}}\nolimits \sqrt[6] x
+C$](img456.gif) .
.
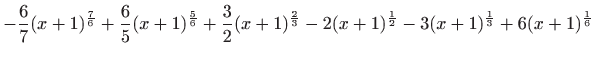
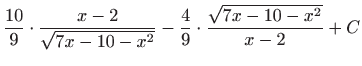 .
.
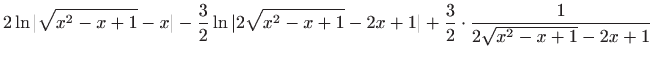
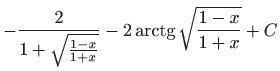 .
.
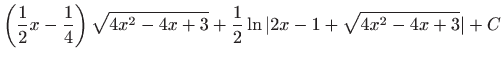 .
.
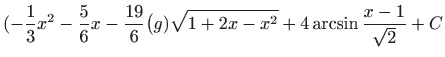 .
.
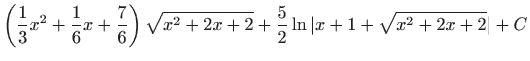 .
.
![$ \displaystyle -\frac{1}{2(\sqrt[4]
x+1)^8}+\frac{4}{9(\sqrt[4] x+1)^9}+C$](img467.gif) .
.
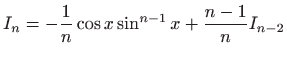 ,
, 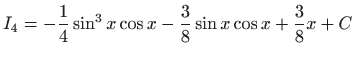 .
.
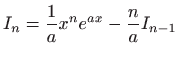 .
.
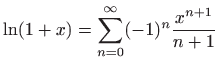 ,
,
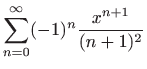 ,
,