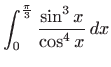
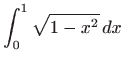
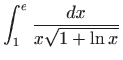
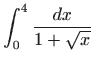
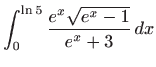
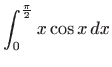
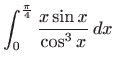
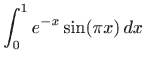
Izračunajte neprave integrale (ili ustanovite njihovu
divergenciju):
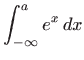
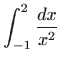
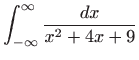
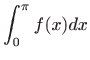 , gdje
je
, gdje
je
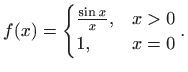 |
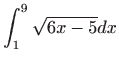 primjenom Simpsonove formule (
primjenom Simpsonove formule (
Izračunajte integrale:
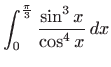
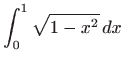
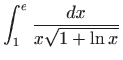
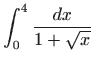
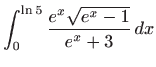
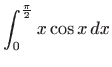
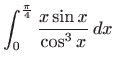
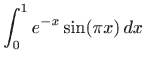
Izračunajte neprave integrale (ili ustanovite njihovu
divergenciju):
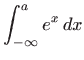
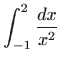
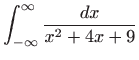
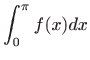 , gdje
je
, gdje
je
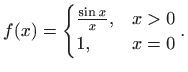 |
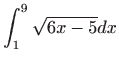 primjenom Simpsonove formule (
primjenom Simpsonove formule (