Izračunajte koordinate težišta homogenog stošca visine ![]() i radijusa baze
i radijusa baze ![]() .
.
Rješenje.
Odredimo najprije jednadžbu stošca.
Opća jednadžba centralnog stošca je
![]() .
Iz
.
Iz ![]() i
i
![]() dobijemo
dobijemo
![]() , odnosno
, odnosno
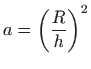 .
Prema tome, jednadžba zadanog stošca je
.
Prema tome, jednadžba zadanog stošca je
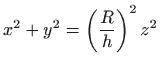 . . |
Prema
![]() [M2, poglavlje 4.5], koordinate težišta su dane sa
[M2, poglavlje 4.5], koordinate težišta su dane sa
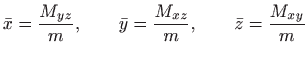 , , |
Stožac ima konstantnu gustoću, što znači da je njegova masa jednaka umnošku gustoće i volumena
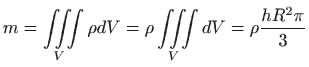 , , |
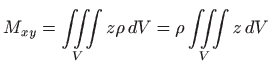 . . |
Prema tome je
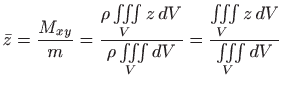 . . |
Uvedimo cilindrične koordinate
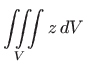 |
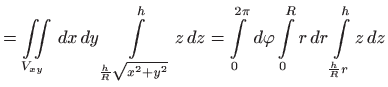 |
|
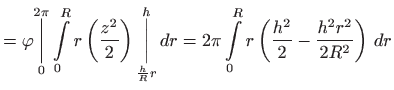 |
||
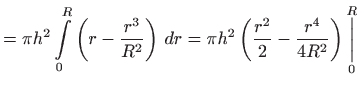 |
||
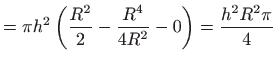 . . |
Dakle,
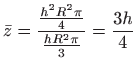 , , |
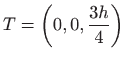 . . |