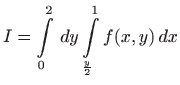 .
.
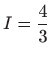 .
.
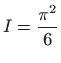 .
.
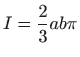 .
.
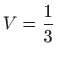 .
.
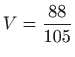 .
.
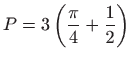 .
.
- a)
-
 ,
,
- b)
-
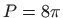 .
.
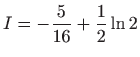 .
.
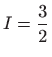 .
.
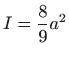 .
.
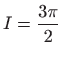 .
.
- a)
-
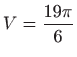 ,
,
- b)
-
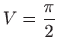 .
.
- a)
-
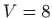 ,
,
- b)
-
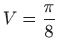 ,
,
- c)
-
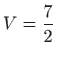 ,
,
- d)
-
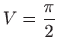 .
.
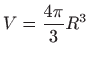 .
.
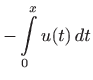 .
.
- a)
- Za funkciju
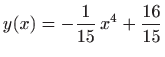 funkcional
postiže lokalni minimum
funkcional
postiže lokalni minimum
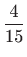 .
.
- b)
- Za funkciju
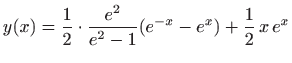 funkcional
postiže lokalni minimum
funkcional
postiže lokalni minimum
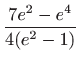 .
.