Neka je zadana funkcija
![]() . Želimo naći funkciju
. Želimo naći funkciju ![]() koja
derivirana daje
koja
derivirana daje ![]() , odnosno želimo riješiti jednadžbu
, odnosno želimo riješiti jednadžbu
za one
Za sljedeću definiciju potrebno je ponoviti neke definicije.
Neka je
![]() ,
, ![]() . Interval
. Interval ![]() je
svaki od skupova
je
svaki od skupova
Ova definicija i činjenica da je derivacija konstantne funkcije jednaka nuli povlače sljedeći teorem.
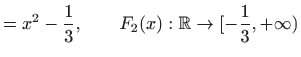 |
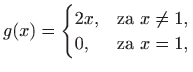
jer možemo uzeti
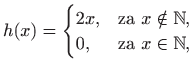 |
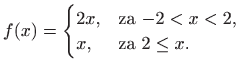 |
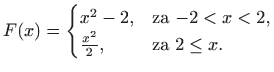 |
Nakon što smo usvojili pojam primitivne funkcije možemo definirati neodređeni integral, no prije toga dokazat ćemo sljedeći teorem.
pa je
Napomenimo da gornju jednakost interpretiramo kao jednakost među
funkcijama, odnosno ![]() označava funkciju
označava funkciju ![]() , a ne njezinu
vrijednost u točki
, a ne njezinu
vrijednost u točki ![]() .
.
Slijedeća dva teorema daju nam osnovna svojstva integrala.
Prisjetimo se
definicije diferencijala
funkcije ![]() (vidi
(vidi
![]() M1, poglavlje 5.2):
M1, poglavlje 5.2):
Prvi teorem navodimo bez dokaza.
vrijedi za svaki
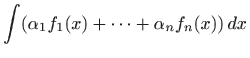 |
||
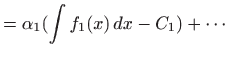 |
||
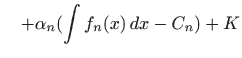 |
||
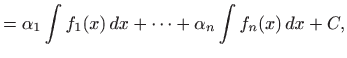 |