U nekim primjenama kao rješavanje problema najmanjih kvadrata kada
matrica ![]() nema puni rang,
nema puni rang,
![]() , koristi se QR rastav s
pivotiranjem stupaca. QR rastav s pivotiranjem
matrice
, koristi se QR rastav s
pivotiranjem stupaca. QR rastav s pivotiranjem
matrice ![]() glasi
glasi
gdje je
Matlab naredba za QR rastav s pivotiranjem matrice
[Q,R,P]=qr(A).
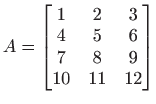
bez pivotiranja i s pivotiranjem.
Octave On-line[Octave On-line Home] [Octave User's Guide] |