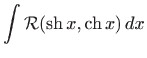
Integrali ove klase funkcija rješavaju se slično kao i integrali racionalnih funkcija trigonometrijskih funkcija iz prethodnog poglavlja. Integral racionalne funkcije hiperbolnih funkcija oblika
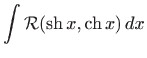
rješavamo koristeći univerzalnu hiperbolnu supstituciju,
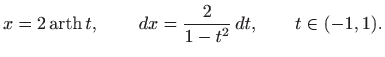
Osnovne veze između hiperbolnih funkcija (vidi
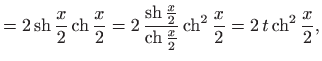 |
||
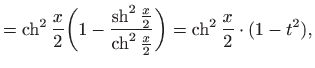 |
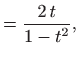 |
||
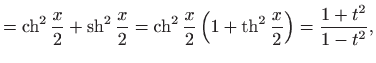 |
||
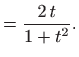 |
Kao i kod trigonometrijskih funkcija i ovdje su u nekim slučajevima moguće jednostavnije supstitucije. Integral oblika
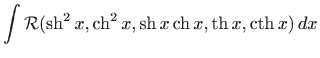
rješavamo pomoću supstitucije
pri čemu vrijedi
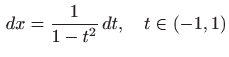 |
||||
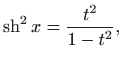 |
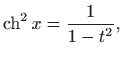 |
|||
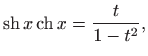 |
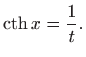 |
Također možemo koristiti i supstitucije
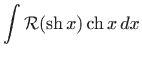 |
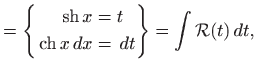 |
|
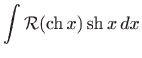 |
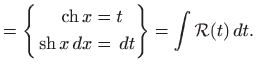 |