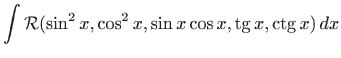
U nekim slučajevima integral racionalne funkcije trigonometrijskih funkcija može se računati pomoću jednostavnijih supstitucije koje vode na integral racionalne funkcije nižeg reda ili pak na jednostavniji integral.
Integral oblika
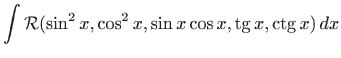
rješavamo pomoću supstitucije
Za
Također možemo koristiti i supstitucije
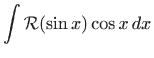 |
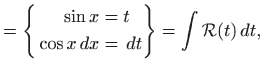 |
|
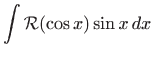 |
 |
 |
||
 |
||
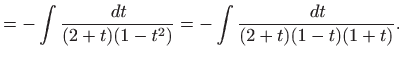 |
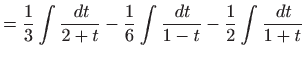 |
||
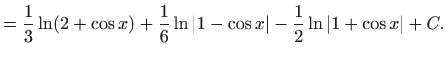 |
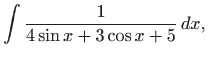 |
||
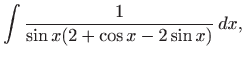 |
||
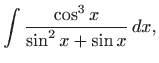 |
||
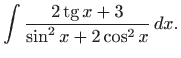 |