Poznato je da se prilikom ronjenja tlak vode povećava s dubinom zarona i to
stoga što se težina vode iznad ronioca povećava. Neka je, na primjer, tanka
horizontalna ploča površine ![]() zaronjena u tekućinu gustoće
zaronjena u tekućinu gustoće
![]() na dubinu od
na dubinu od ![]() metara ispod površine tekućine (slika
2.26).
metara ispod površine tekućine (slika
2.26).
Tekućina koja se nalazi direktno iznad ploče ima volumen ![]() pa je njena
masa jednaka
pa je njena
masa jednaka
![]() . Sila kojom ta količina vode djeluje na
ploču jednaka je
. Sila kojom ta količina vode djeluje na
ploču jednaka je
pri čemu je
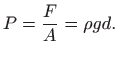
Jedinica za mjerenje tlaka je paskal, odnosno njutn po metru kvadratnom (pascal,
Eksperimentalno je utvrđeno da je na svakom mjestu u tekućini pritisak jednak u svim smjerovima.
Za bolje razumijevanje hidrostatskog pritiska, izračunajmo pritisak vode na branu prikazanu na slici 2.27.
Brana ima oblik trapeza, visoka je
![]() , široka je
na vrhu
, široka je
na vrhu
![]() , a na dnu
, a na dnu
![]() . Zrcalo vode se nalazi
. Zrcalo vode se nalazi
![]() ispod vrha brane. Ako postavimo koordinatnu
ispod vrha brane. Ako postavimo koordinatnu
![]() -os tako da se ishodište nalazi na površini vode, dubina vode je
-os tako da se ishodište nalazi na površini vode, dubina vode je
![]() . Neka je
. Neka je
![]() podjela intervala
podjela intervala ![]() takva da su svi podintervali jednake duljine,
takva da su svi podintervali jednake duljine,
![]() .
Sada je
.
Sada je ![]() -ti podjeljak brane približno jednak pravokutniku visine
-ti podjeljak brane približno jednak pravokutniku visine ![]() i širine
i širine
![]() . Iz sličnosti trokuta slijedi
. Iz sličnosti trokuta slijedi
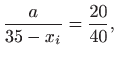
iz čega slijedi
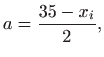
pa je
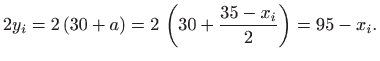
Površina
Kako je
Hidrostatska sila koja djeluje na
Zbrajanjem ovih sila i uzimanjem limesa kada
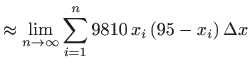 |
||
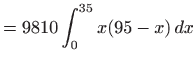 |
||
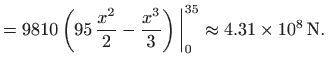 |