×   HOME PREDAVANJA

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA INDEKS

VJEŽBE

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

PODSJETNIK

SADRŽAJ NEODREĐENI INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

JAVA NETPLOT OCTAVE Traži ...

☰   matematika2 FUNKCIJE VIŠE VARIJABLA     FUNKCIJE VIŠE VARIJABLA     Limes

Definicija

Definicija 3.1   Skup $\mathbb{R}^n=\mathbb{R}\times\cdots\times\mathbb{R}$ ($n$ -terostruki Kartezijev produkt skupa realnih brojeva sa samim sobom), odnosno

$$\mathbb{R}^n=\{(x_1,x_2,\cdots,x_n) \vert x_i\in\mathbb{R}, i=1,2,\cdots,n\}$$

zovemo $n$ -dimenzionalni Euklidski prostor, a uređene $n$ -torke $(x_1,x_2,\cdots,x_n)$ su točke tog prostora. Preslikavanje $f:D\to \mathbb{R}$ , $D\subseteq\mathbb{R}^n$ koje svakoj točki područja definicije $D$ pridružuje realan broj zovemo realna funkcija od $n$ realnih varijabla. Koristimo oznaku $T\to f(T), T\in D$ ili

$$(x_1,x_2,\cdots,x_n)\to f(x_1,x_2,\cdots,x_n),\ (x_1,x_2,\cdots,x_n)\in D$$

Za razliku od realne funkcije jedne realne varijable (slučaj $n=1$ ) kad god imamo funkciju od $n$ varijabla s $n>1$ govorimo o funkciji više varijabla. Takve funkcije možemo kao i u jednodimenzionalnom slučaju zadavati eksplicitnim analitičkim izrazom, tablicom (u slučaju diskretnog područja definicije), grafički (u slučaju $n=2$ ), parametarskim jednadžbama i implicitnim analitičkim izrazom.

Primjer 3.1   Eksplicitnom formulom $z=\sqrt{x^2+y^2}$ definirana je jedna realna funkcija dviju varijabla čije je prirodno područje definicije

$$D=\{(x,y)\in \mathbb{R}^2\vert x^2+y^2\ge 0\}\equiv\mathbb{R}^2.$$

Da bi funkciju predočili grafički koristimo projekcije na koordinatne ravnine. Sustavom $y=0, z=\sqrt{x^2+y^2}$ određena je jednadžba $z=\sqrt{x^2}=\vert x\vert$ projekcije na $xz$ -ravninu (vidi sliku 3.1).

Slika: Projekcija kružnog stošca na $xz$ -ravninu

Slično, sustavom $x=0, z=\sqrt{x^2+y^2}$ određena je jednadžba $z=\sqrt{y^2}=\vert y\vert$ projekcije na $yz$ -ravninu, a dok za $x=1$ jednadžba projekcije glasi $z=\sqrt{1+y^2}$ (vidi sliku 3.2).

Slika: Projekcije kružnog stošca na $yz$ -ravninu

Napokon, za zadani $z_0>0$ sustavom $z=z_0, z=\sqrt{x^2+y^2}$ određena je jednadžba $x^2+y^2=z_0^2$ što pokazuje da je presjek grafa zadane funkcije s ravninom $z=z_0$ jedna kružnica polumjera $z_0$ (vidi sliku 3.3)

Slika: Projekcije kružnog stošca na $xy$ -ravninu

Nacrtamo li sustavno prethodne projekcije, dobit ćemo sliku 3.4^3.1Zaključujemo da je graf funkcije kružni stožac kojemu je ishodište $(0,0,0)$ vrh, a $Oz$ -os os simetrije.

Slika: Kružni stožac

Općenito

$$z-z_0=\sqrt{a^2(x-x_0)^2+b^2(y-y_0)^2}$$

je eliptički stožac s vrhom u točki $(x_0,y_0,z_0)$ , a presjek tog stošca s ravninom $z=c$ ($c>z_0$ ) je elipsa

$$\frac{(x-x_0)^2}{\left(\frac{c-z_0}{a}\right)^2}+\frac{(y-y_0)^2} {\left(\frac{c-z_0}{b}\right)^2}=1$$

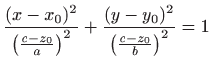
Na primjer, na slici 3.5 prikazan je eliptički stožac

$$z-3=\sqrt{\frac{1}{4}(x+1)^2+\frac{1}{9}(y-2)^2}.$$

Slika: Eliptički stožac

Napomena 3.1   Jednadžbama $f(x_1,\ldots,x_n)=c$ , gdje je $c$ konstanta, određene su takozvane nivo plohe koje služe za lakše predočavanje grafa funkcije. U slučaju $n=2$ nivo plohe još zovemo nivo krivulje i crtamo ih u istoj ravnini. Na slici 3.3 vidimo nekoliko nivo krivulja funkcije $z=\sqrt{x^2+y^2}$ . Na slici 3.5 nacrtane su nivo krivulje u $xy$ -ravnini. Još su zanimljivije, na primjer, izohipse (krivulje na zemljopisnim kartama koje povezuju točke iste nadmorske visine ili morske dubine) ili izobare (krivulje na meteorološkim kartama koje povezuju točke jednakog atmosferskog pritiska). Primjer izobara na slici 3.6 preuzet je s web stranica Državnog hidrometeorološkog zavoda.

Slika 3.6: Izobare vremenske prognoze

Primjer 3.2  

a)

Funkcija $z=\ln{(x+y-2)}$ definirana je na području $\mathcal{D}\subseteq \mathbb{R}^2$ određenom nejednakošću $x+y-2>0$ (vidi sliku 3.7).

Slika: Područje definicije funkcije

b)

Formulom $u=\arcsin (x^2+y^2+z^2-2)$ zadana je jedna funkcija triju varijabla definirana na području $\mathcal{D}\subseteq \mathbb{R}^3$ koje je određeno nejednakostima $-1\leq x^2+y^2+z^2-2\leq 1$ , odnosno

$$D=\{(x,y,z)\in\mathbb{R}^3 \mid 1\leq x^2+y^2+z^2\leq 3\}.$$

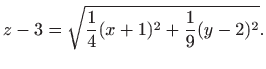
Nivo-plohe su plaštevi kugli (vidi sliku 3.8). Nivo-plohe su nacrtane koristeći parametarski prikaz funkcije tri varijable.

Slika 3.8: Nivo-plohe

c)

Funkcija triju varijabla $u=-\frac{x^2+y^2}{z}$ definirana je za

$$(x,y,z)\in \mathbb{R}^3\setminus\{(x,y,0)\mid (x,y)\in\mathbb{R}^2 \}.$$

Nivo-plohe su kružni paraboloidi (bez tjemena). Na primjer za $u=1$ dobijamo $z=-(x^2+y^2)$ . Presjek s ravninom $x=0$ je parabola $z=-y^2$ , presjek s ravninom $y=0$ je parabola $z=-x^2$ , a presjek s ravninom $z=-1$ je kružnica $x^2+y^2=1$ . Nivo-plohe za $u=1$ i $u=2$ su prikazane na slici 3.9. Općenito, $z-z_0=a^2(x-x_0)^2+b^2(y-y_0)^2$ prema gore okrenut je eliptički paraboloid s vrhom u točki $(x_0,y_0,z_0)$ , a $z-z_0=-a^2(x-x_0)^2-b^2(y-y_0)^2$ prema dolje okrenut je eliptički paraboloid s vrhom u točki $(x_0,y_0,z_0)$ .

Slika 3.9: Nivo-plohe

Zadatak 3.1   Nacrtajte slike 3.4, 3.8 i 3.9 pomoću programa NetPlot.

Za crtanje funkcija dviju varijabla možete koristiti i java aplet.

Definicija 3.2   Funkcija $f$ je omeđena ako postoji $M>0$ takav da je

$$\vert f(T)\vert\leq M, \forall T\in \mathcal{D}.$$

Definicija 3.3   Neka je zadana funkcija $f:\mathcal{D}\to\mathbb{R}$ . Ako svim varijablama osim jedne, recimo $x_i$ , pridružimo konkretne vrijednosti

$$x_1=x_1^0,\cdots,x_{i-1}=x_{i-1}^0,x_{i+1}=x_{i+1}^0,\cdots,x_n=x_n^0,$$

onda možemo definirati funkciju jedne varijable $f_i: \mathcal{D}_i\to\mathbb{R}$ , $\mathcal{D}_i\subseteq \mathbb{R}$ formulom

$$f_i(x)=f(x_1^0,\cdots,x_{i-1}^0,x,x_{i+1}^0,\cdots,x_n^0).$$

Kažemo da je funkcija $f$ rastuća (strogo rastuća, padajuća, strogo padajuća) s obzirom na varijablu $x_i$ za $x_1=x_1^0,\cdots,x_{i-1}=x_{i-1}^0,x_{i+1}=x_{i+1}^0,\cdots,x_n=x_n^0$ ako je funkcija $f_i$ takva.

Primjer 3.3   Neka je $z=f(x,y)=2 x^3-y^2$ i neka je zadana točka $T=(1,2)$ . Tada je funkcija $f_1(x)=f(x,2)=2 x^3-4$ strogo rastuća, dok je funkcija $f_2(y)=f(1,y)=2-y^2$ strogo rastuća za $y\leq 0$ i strogo padajuća za $y>0$ .

FUNKCIJE VIŠE VARIJABLA     FUNKCIJE VIŠE VARIJABLA     Limes