- ...
(vidi1.1
- Reference označene s M1
odnose se na udžbenik: I. Slapničar, Matematika 1, FESB, Split, 2001.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....1.2
- Ako je
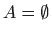 , onda je
, onda je 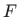 striktno primitivna funkcija
funkcije
striktno primitivna funkcija
funkcije 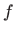 na intervalu
na intervalu 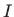 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... parametra.1.3
- Jedan oblik rekurzivne
formule u kojoj smo integral izrazili pomoću istog izraza imali smo u primjeru
1.6 d).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...1.4
- Vidi
http://www.wolframalpha.com/calculators/integral-calculator/.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
supstitucije1.5
- Radi se o svođenju
izraza pod korijenom na puni kvadrat - vidi primjer.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... s2.1
- Koristimo skraćene oznake
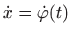 i
i
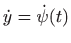 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... formulom2.2
- Koristimo skraćene oznake
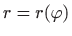 i
i
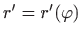 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... teorem2.3
- Teorem navodimo bez dokaza. Dokaz je sličan dokazu
teorema 2.6 s time što funkciju
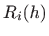 treba derivirati tri
puta nakon čega treba primijeniti teorem srednje vrijednosti i dva puta
integrirati.
treba derivirati tri
puta nakon čega treba primijeniti teorem srednje vrijednosti i dva puta
integrirati.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... On-line2.4
- http://lavica.fesb.unist.hr/octave/ool_hr.php.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...fig:vv3a3.1
- Projekcije crtamo kao parametarski zadane krivulje u
prostoru, odnosno crtamo krivulje
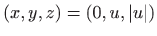 ,
,
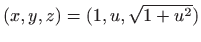 ,
,
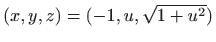 ,
,
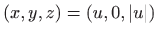 ,
,
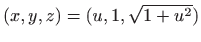 ,
,
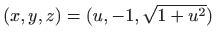 ,
,
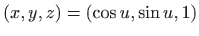 ,
,
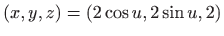 i
i
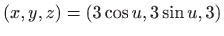 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... koeficijenata3.2
- Svi koeficijenti
su realni brojevi.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
kružnice.3.3
- U rubovima je nivo-krivulja ili pak presjek s ravninom
koja je paralelna s
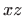 - ili
- ili 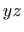 -ravninom jednaka točki koju možemo
interpretirati kao degeneriranu kružnicu s polumjerom 0
.
-ravninom jednaka točki koju možemo
interpretirati kao degeneriranu kružnicu s polumjerom 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....3.4
- Drugim
riječima, jedan od prva dva slučaja je narušen sa strogom nejednakošću.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....3.5
- Drugim
riječima, jedan od prva dva slučaja je narušen sa jednakošću s nulom.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....4.1
- Funkcija
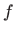 je također omeđena na zatvorenom skupu
je također omeđena na zatvorenom skupu
![$ [a,b]\times [c,d]$](img2058.gif) po svojstvu (ii) iz poglavlja
3.3.
po svojstvu (ii) iz poglavlja
3.3.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... krivuljom4.2
- Krivulja je glatka, što znači da
se sastoji od konačno glatkih dijelova; krivulja je jednostavna, što znači
da ne presijeca samu sebe; i krivulja je zatvorena, što znači da
počinje i završava u istoj točki.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...\space 4.3
- Za više informacija vidi
http://www.wikipedia.org/wiki/Normal_distribution.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
područja4.4
- Integriranje ove formule po varijabli
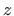 daje formulu
4.1.
daje formulu
4.1.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... izostavljamo4.5
- Usporedi s izvodom elementa površine
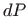 u polarnim koordinatama iz poglavlja 4.2.2.
u polarnim koordinatama iz poglavlja 4.2.2.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... vrijedi4.6
- Uvjerite se u ovu tvrdnju tako
što ćete izračunati moment
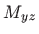 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...brahistohrona.4.7
- Na grčkom jeziku brahistos znači
najkraći, a hronos znači vrijeme. Problem je 1696. godine postavio Johann
Bernoulli, a riješio ga je iste godine
Isaac Newton.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
4.3)4.8
- Prethodni integral riješili smo koristeći nestandardnu supstituciju iz
koje se odmah vidi da rješenje ima oblik cikloide. Integral se može riješiti
i pomoću standardne racionalne supstitucije
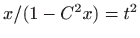 (vidi
poglavlje 1.7.1).
(vidi
poglavlje 1.7.1).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... bisekcije4.9
- Vidi, na
primjer, Java program
http://lavica.fesb.unist.hr/matematika1/java/Bisekcija.html.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... godine5.1
- Podaci
su preuzeti s adrese
http://en.wikipedia.org/wiki/World_population.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... godine5.2
- Vidi
http://www.wikipedia.org/wiki/Radium.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ekvivalentne5.3
- Drugim riječima,
ako je bilo koja tvrdnja istinita, onda su istinite i ostale.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...fig:mot.5.4
- Sustav je složeniji od sustava opisanog u primjeru 5.1.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
uvjetima5.5
- O početnim uvjetima ovise konstante
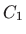 i
i 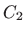 , no
taj dio rješenja nestaje u beskonačnosti.
, no
taj dio rješenja nestaje u beskonačnosti.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... godine5.6
- Vidi
http://en.wikipedia.org/wiki/Tacoma_Narrows_Bridge.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Londonu5.7
- Vidi
http://en.wikipedia.org/wiki/London_Millennium_Bridge.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....5.8
- Opravdanost ovog
postupka dokazujemo tako da funkciju
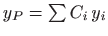 deriviramo
deriviramo
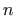 puta koristeći pri tome jednakosti iz zadanog sustava te potom uvrstimo
u jednadžbu (5.27).
puta koristeći pri tome jednakosti iz zadanog sustava te potom uvrstimo
u jednadžbu (5.27).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...fig:eulrvz.5.9
- Radi preglednije slike broj zečeva je
podijeljen s deset, odnosno nacrtane su funkcije
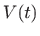 i
i 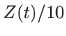 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... nepoznanice6.1
- Izvod ove jednadžbe dan je u sljedećem
poglavlju.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... statistiku6.2
- Vidi http://www.dzs.hr.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.