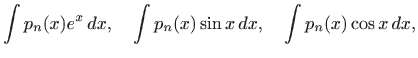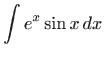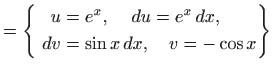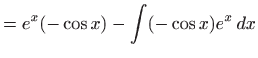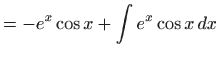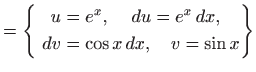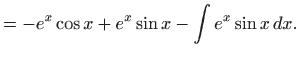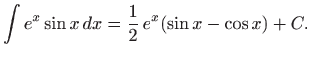☰
matematika2
Metode supstitucije
NEODREĐENI INTEGRAL
Rekurzivne formule
Metoda parcijalne integracije
Ova metoda sastoji se od povoljnog rastavljanja zadanog
integrala u obliku
i primjene sljedećeg teorema.
Teorem 1.7 Ako su funkcije
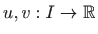
derivabilne na intervalu
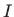
,
onda vrijedi
formula parcijalne integracije
Dokaz.
Neka je 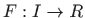 primitivna funkcija funkcije
primitivna funkcija funkcije
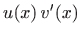 na
intervalu
na
intervalu 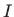 , odnosno
, odnosno 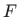 je neprekidna i vrijedi
je neprekidna i vrijedi
pri čemu je
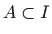 diskretan podskup. Zbog derivabilnosti
funkcija
diskretan podskup. Zbog derivabilnosti
funkcija 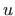 i
i 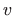 je i funkcija
je i funkcija
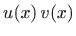 neprekidna na intervalu
neprekidna na intervalu 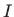 .
Stoga je funkcija
.
Stoga je funkcija
neprekidna na intervalu 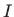 te za svaki
te za svaki
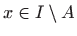 vrijedi
vrijedi
Dakle, 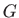 je primitivna funkcija funkcije
je primitivna funkcija funkcije 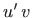 na intervalu
na intervalu 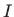 pa je
pa je
i teorem je dokazan.
Q.E.D.
Izbor funkcija 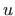 i
i 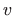 je stvar iskustva. Tvrdnju teorema 1.7 možemo
zapisati u kraćem obliku:
je stvar iskustva. Tvrdnju teorema 1.7 možemo
zapisati u kraćem obliku:
Primjer 1.6
- a)
- Vrijedi
Prilikom rješavanja pomoćnog integrala
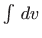 nije potrebno pisati
konstantu integracije,
jer je dovoljna jedna konstanta integracije
nije potrebno pisati
konstantu integracije,
jer je dovoljna jedna konstanta integracije 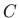 na kraju zadatka.
na kraju zadatka.
- b)
- Za funkciju
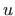 možemo uzeti i čitavu podintegralnu funkciju
ukoliko se ona deriviranjem pojednostavni:
možemo uzeti i čitavu podintegralnu funkciju
ukoliko se ona deriviranjem pojednostavni:
- c)
- Formulu parcijalne integracije možemo primijeniti više puta
uzastopce:
Općenito, zaključujemo da integrale oblika
gdje je 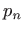 polinom
polinom 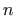 -tog stupnja,
možemo riješiti primjenom parcijalne integracije
-tog stupnja,
možemo riješiti primjenom parcijalne integracije 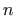 puta za redom.
puta za redom.
- d)
- Integrale sljedećeg tipa rješavamo tako da nakon dvostruke
parcijalne integracije dobijemo izraz koji opet sadrži polazni
integral:
Iz prethodne jednakosti slijedi
Primijetimo da smo zbog svojevrsne simetrije zadatak mogli riješiti i
pomoću rastava 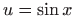 i
i
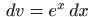 .
.
Poglavlja
Metode supstitucije
NEODREĐENI INTEGRAL
Rekurzivne formule
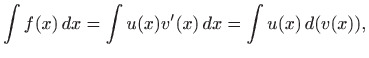
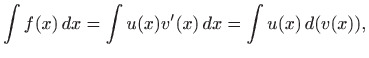
![]() i
i ![]() je stvar iskustva. Tvrdnju teorema 1.7 možemo
zapisati u kraćem obliku:
je stvar iskustva. Tvrdnju teorema 1.7 možemo
zapisati u kraćem obliku:
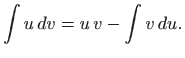
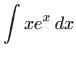
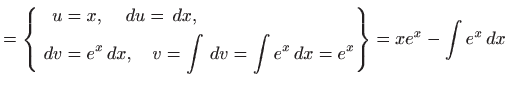
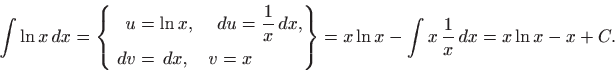
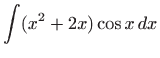
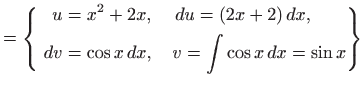
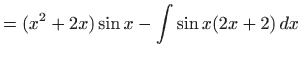
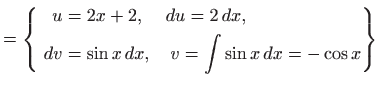
![$\displaystyle = (x^2+2x)\sin x - \bigg[ (2x+2)(-\cos x) - \int (-\cos x) 2 dx\bigg]$](img258.gif)