Za rješavanje složenijih integrala često koristimo dvije metode supstitucije. One se sastoje u tome da se zadani integral
Drugim riječima,
![]() možemo rješavati pomoću supstitucije
možemo rješavati pomoću supstitucije
![]() , pri čemu je
, pri čemu je ![]() bijekcija:
bijekcija:
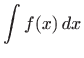 |
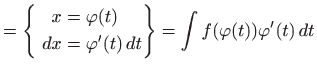 |
|
Zbog bijektivnosti funkcije
Dakle, za
Neka je
pri čemu je
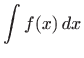 |
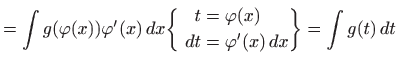 |
|
odnosno
Integrale u primjeru 1.5 a), b) i c) smo formalno mogli riješiti i koristeći teorem 1.5, odnosno pomoću supstitucija
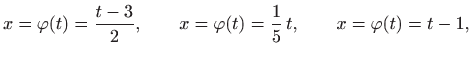
redom, koje su sve bijekcije na skupu