Višestruki integral (ili ![]() -terostruki
integral je integral funkcije
-terostruki
integral je integral funkcije ![]() varijabla
koja je definirana na zatvorenom
varijabla
koja je definirana na zatvorenom ![]() -dimenzionalnom
kvadru
-dimenzionalnom
kvadru
a definira se slično određenom integralu funkcija
jedna podjela segmenta
zove se podjela (rastav ili dekompozicija) kvadra
Neka je
![]() omeđena funkcija, to jest, neka postoje
omeđena funkcija, to jest, neka postoje
![]() takvi
da je
takvi
da je
Tada svakoj podjeli
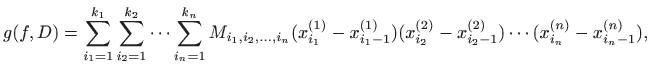
gdje je
i donju integralnu sumu
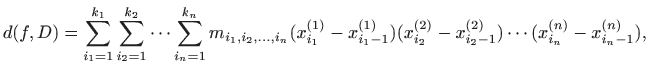
gdje je
Ako je
broj
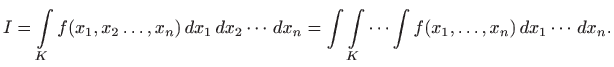
Definiciju ćemu ilustrirati sljedećim primjerom.
Zadana funkcija na svakom dijelu
![]() očito postiže maksimum u prednjem lijevom uglu, a minimum u stražnjem desnom
uglu,
očito postiže maksimum u prednjem lijevom uglu, a minimum u stražnjem desnom
uglu,
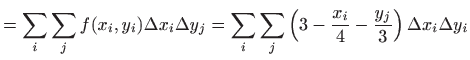 |
||
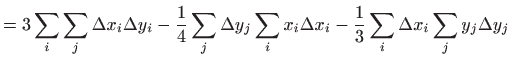 |
||
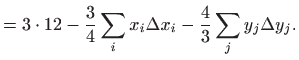 |
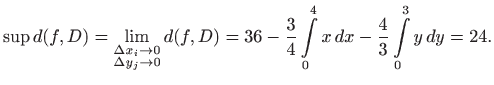
Na sličan se način pokaže da je
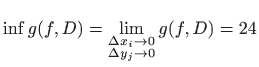
pa je zadana funkcija integrabilna na kvadru
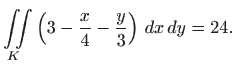
Ako područje integracije nije kvadar, višestruki integral definiramo na sljedeći način:
Iz prethodnih definicija slijede osnovna
svojstva višestrukog integrala. Za
funkcije ![]() i
i ![]() koje su integrabilne na području
koje su integrabilne na području ![]() vrijedi:
vrijedi:
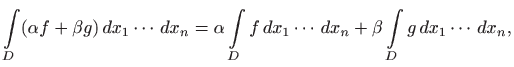
gdje su
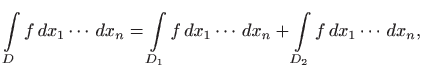
gdje je