Izogonalna trajektorija
obitelji (ili familije) krivulja
![]() ovisne o parametru
ovisne o parametru ![]() je svaka
krivulja koja siječe svaku krivulju zadane obitelji pod zadanim kutom. Ukoliko
je kut pravi, radi se o ortogonalnoj trajektoriji.
je svaka
krivulja koja siječe svaku krivulju zadane obitelji pod zadanim kutom. Ukoliko
je kut pravi, radi se o ortogonalnoj trajektoriji.
Na primjer, ako je zadana obitelj pravaca koji prolaze kroz ishodište,
![]() ,
,
![]() , onda je svaka kružnica sa središtem u ishodištu,
, onda je svaka kružnica sa središtem u ishodištu,
![]() ,
,
![]() , ortogonalna trajektorija te obitelji (vidi
sliku 5.10). Kažemo da su dvije obitelji ortogonalne trajektorije
jedna drugoj.
, ortogonalna trajektorija te obitelji (vidi
sliku 5.10). Kažemo da su dvije obitelji ortogonalne trajektorije
jedna drugoj.
Ortogonalne trajektorije možemo, ako postoje, naći sljedećim postupkom:
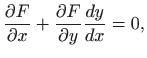
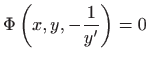
pa je rješenje ove jednadžbe jednadžba obitelji ortogonalnih trajektorija.
pri čemu smo koristili pravilo o deriviranju složene funkcije. Kako je
Dakle, ortogonalne trajektorije zadovoljavaju jednadžbu
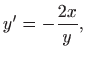
odnosno,
Integriranje daje
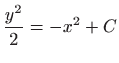
pa su ortogonalne trajektorije elipse sa središtem u ishodištu (vidi sliku 5.11),
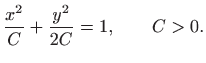
Postupak računanje izogonalnih trajektorija proizlazi iz sljedećeg zapažanja:
ako je
![]() koeficijent smjera tangente na zadanu krivulju i
ako je
koeficijent smjera tangente na zadanu krivulju i
ako je
![]() koeficijent smjera tangente izogonalne trajektorije
koja zadanu krivulju siječe pod kutom
koeficijent smjera tangente izogonalne trajektorije
koja zadanu krivulju siječe pod kutom ![]() ,
onda vrijedi (vidi sliku 5.12)
,
onda vrijedi (vidi sliku 5.12)
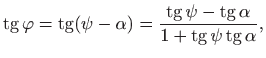
odnosno,
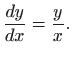
U ovom slučaju je
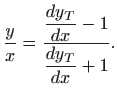
Ispuštanje indeksa
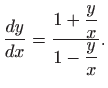
Ovo je homogena diferencijalna jednadžba čije rješenje glasi
U polarnim koordinatama
pa rješenje glasi
odnosno
što je jednadžba obitelji logaritamskih spirala (vidi sliku 5.13).