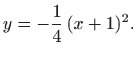Opće rješenje diferencijalne jednadžbe prvog reda oblika
skup je funkcija
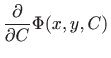 |
Vrijedi
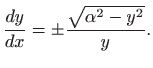
Separacija varijabli daje
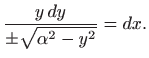
pa je rješenje jednadžbe obitelj kružnica radijusa
Ovojnice ove obitelji su pravci
Singularno rješenje smo mogli dobiti i pomoću svojstva S3: jednakost
povlači
Clairautova diferencijalna jednadžba glasi
Deriviranje jednadžbe daje
odnosno
Izjednačavanje prvog faktora s nulom daje
što je obitelj pravaca ovisna o parametru
Na primjer, uz supstituciju
je
dok je singularno rješenje jednako (vidi sliku 5.15)