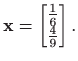Metodom najmanjih kvadrata pomoću QR rastava riješite sustav
![]() , gdje je
, gdje je
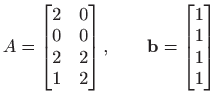 . . |
Rješenje.
Pronađimo najprije QR rastav matrice ![]() . Stupac
. Stupac
![]() trebamo zarotirati u
vektor
trebamo zarotirati u
vektor
![]() jer je
jer je
![]() . Vrijedi
. Vrijedi
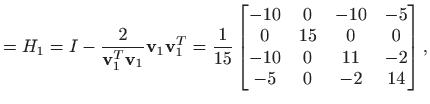 |
||
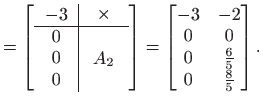 |
Sada pronađimo Householderov reflektor ![]() pridružen vektoru
pridružen vektoru
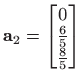 .
Norma vektora
.
Norma vektora
![]() je
je
![]() , što
znači da vektor
, što
znači da vektor
![]() treba zarotirati u
treba zarotirati u
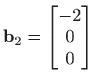 .
Dakle,
.
Dakle,
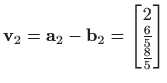 i
i 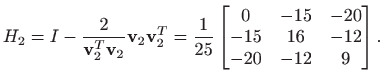
Stavimo
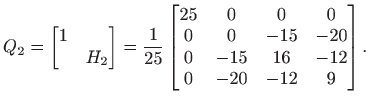
Sada je
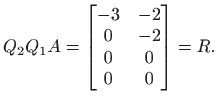
Matrica
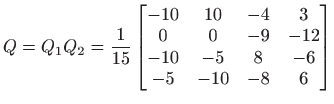
pa QR rastav matrice
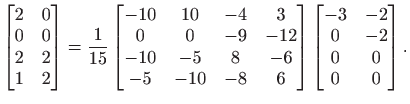
Riješimo sada sustav ![]() .
Zamijenimo li
.
Zamijenimo li ![]() s
s ![]() , zbog ortogonalnosti matrice
, zbog ortogonalnosti matrice ![]() vrijedi
vrijedi
odnosno
Prema
gdje je
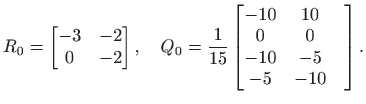
Vrijedi
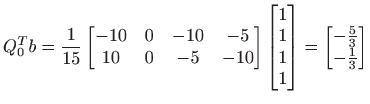
pa je rješenje sustava
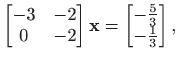
a time ujedno i rješenje polaznog sustava u smislu najmanjih kvadrata