☰
matematika2
Rješavanje problema najmanjih kvadrata
METODA NAJMANJIH KVADRATA I
Rješenja zadataka za vježbu
Zadaci za vježbu
- 1.
- Metodom najmanjih kvadrata nađite funkciju oblika
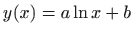 koja aproksimira sljedeći skup podataka (točaka):
koja aproksimira sljedeći skup podataka (točaka):
- 2.
- Metodom najmanjih kvadrata nađite funkciju oblika
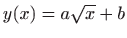 koja aproksimira sljedeći skup podataka (točaka):
koja aproksimira sljedeći skup podataka (točaka):
- 3.
- Izračunajte QR rastav matrice
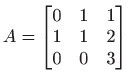 . . |
|
- 4.
- Neka je
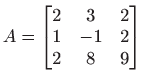 .
.
- a)
- Izračunajte QR rastav matrice
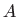 .
.
- b)
- Koristeći QR rastav riješite sustav
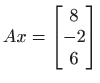 .
.
- 5.
- Neka je
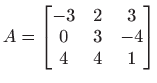 .
.
- a)
- Izračunajte QR rastav matrice
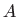 .
.
- b)
- Koristeći QR rastav, riješite sustav
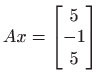 .
.
- 6.
- Neka je
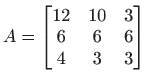 .
.
- a)
- Izračunajte QR rastav matrice
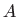 .
.
- b)
- Koristeći QR rastav riješite sustav
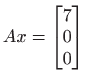 .
.
- 7.
- Zadane su točke u ravnini:
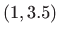 ,
, 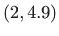 ,
, 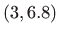 ,
, 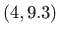 ,
, 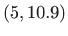 ,
, 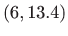 ,
, 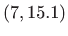 ,
, 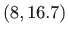 ,
, 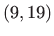 .
Aproksimirajte točke pravcem
.
Aproksimirajte točke pravcem
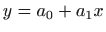 metodom najmanjih kvadrata koristeći QR rastav matrice.
metodom najmanjih kvadrata koristeći QR rastav matrice.
- 8.
- Odredite
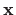 koji minimizira normu
koji minimizira normu
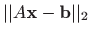 koristeći metodu najmanjih kvadrata uz pomoć QR rastava ako je
koristeći metodu najmanjih kvadrata uz pomoć QR rastava ako je
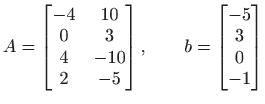 . . |
|
Rješavanje problema najmanjih kvadrata
METODA NAJMANJIH KVADRATA I
Rješenja zadataka za vježbu
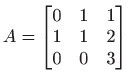 .
. 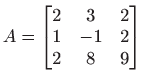 .
.
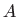 .
.
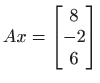 .
.
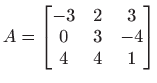 .
.
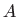 .
.
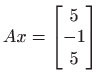 .
.
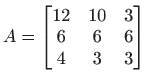 .
.
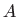 .
.
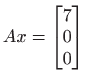 .
.
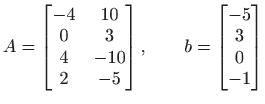 .
.