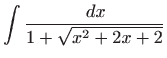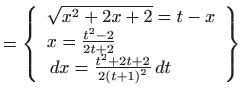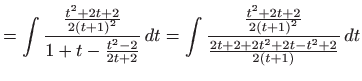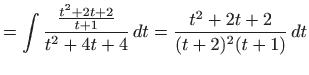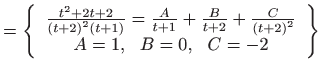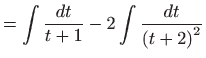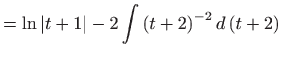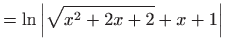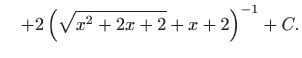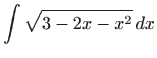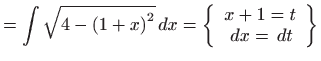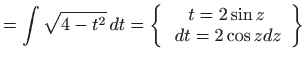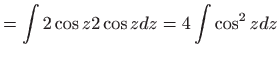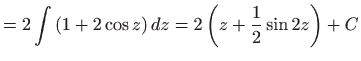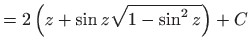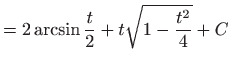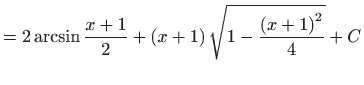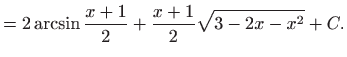☰
matematika2
Integriranje iracionalnih funkcija racionalnom
NEODREĐENI INTEGRAL
Metoda neodređenih koeficijenata
Eulerova i trigonometrijska supstitucija
Izračunajte integrale:
- a)
-
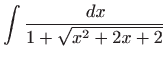 ,
,
- b)
-
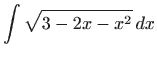 ,
,
Rješenje.
- a)
- Koristimo
Eulerovu supstituciju
![[*]](../icons.gif/crossref.gif) [M2, poglavlje 1.7.2]. Vrijedi
[M2, poglavlje 1.7.2]. Vrijedi
- b)
- Izraz pod korijenom nadpounjavamo do punog kvadrata, a zatim
uvodimo dvije supstitucije:
Integriranje iracionalnih funkcija racionalnom
NEODREĐENI INTEGRAL
Metoda neodređenih koeficijenata
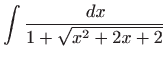 ,
,
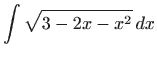 ,
,
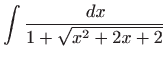 ,
,
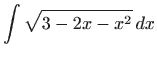 ,
,