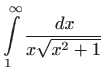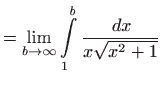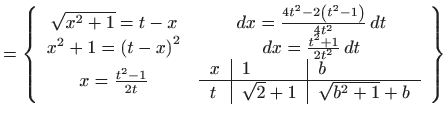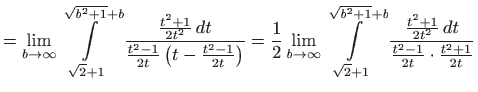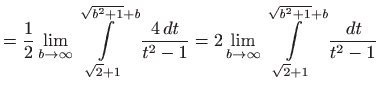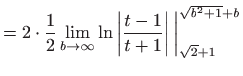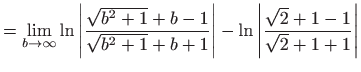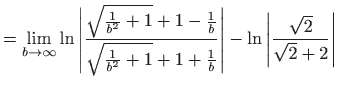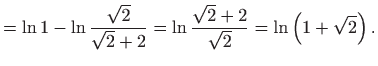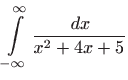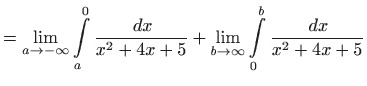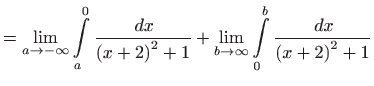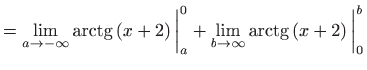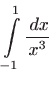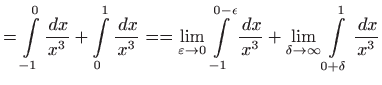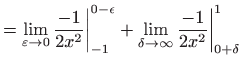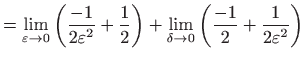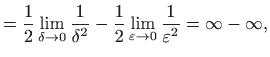☰ matematika2

Supstitucija i parcijalna integracija ODREĐENI INTEGRAL Površina ravninskog lika

Nepravi integral

Izračunajte slijedeće integrale:

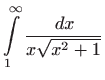a): $\displaystyle\int\limits_{1}^{\infty }\frac{ dx}{x\sqrt{x^{2}+1}}$ ,
b)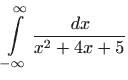: $\displaystyle\int\limits_{-\infty }^{\infty }\frac{ dx}{x^{2}+4x+5}$ ,
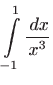c): $\displaystyle\int\limits_{-1}^{1}\frac{ dx}{x^{3}}$ .

Rješenje.

a)

Vrijedi

$\displaystyle \int\limits_{1}^{\infty }\frac{ dx}{x\sqrt{x^{2}+1}}$	$\displaystyle =\lim_{b\rightarrow \infty }\int\limits_{1}^{b}\frac{ dx}{x\sqrt{x^{2}+1}}$
	$\displaystyle =\left\{ \begin{array}{cc} \sqrt{x^{2}+1}=t-x & dx=\frac{4t^{2}... ...ne $t$ & $\sqrt{2}+1$ & $\sqrt{b^{2}+1}+b$ \end{tabular} \end{array} \right\}$
	$\displaystyle =\lim_{b\rightarrow \infty }\int\limits_{\sqrt{2}+1}^{\sqrt{b^{2}... ...b}\frac{\frac{t^{2}+1}{2t^{2}} dt}{\frac{t^{2}-1}{2t}\cdot \frac{t^{2}+1}{2t}}$
	$\displaystyle =\frac{1}{2}\lim_{b\rightarrow \infty }\int\limits_{\sqrt{2}+1}^{... ...tarrow \infty }\int\limits_{ \sqrt{2}+1}^{\sqrt{b^{2}+1}+b}\frac{ dt}{t^{2}-1}$
	$\displaystyle =2\cdot \frac{1}{2}\lim_{b\rightarrow \infty }\ln \left\vert \frac{t-1}{t+1 }\right\vert \bigg\vert_{\sqrt{2}+1}^{\sqrt{b^{2}+1}+b}$
	$\displaystyle =\lim_{b\rightarrow \infty }\ln \left\vert \frac{\sqrt{b^{2}+1}+b... ...}+b+1}\right\vert -\ln \left\vert \frac{\sqrt{2}+1-1}{\sqrt{2}+1+1} \right\vert$
	$\displaystyle =\lim_{b\rightarrow \infty }\ln \left\vert \frac{\sqrt{\frac{1}{b... ...+\frac{1}{b}}\right\vert -\ln \left\vert \frac{\sqrt{2}}{\sqrt{2}+2}\right\vert$
	$\displaystyle =\ln 1-\ln \frac{\sqrt{2}}{\sqrt{2}+2}=\ln \frac{\sqrt{2}+2}{\sqrt{2}}=\ln \left( 1+\sqrt{2}\right) .$

b)

Vrijedi

$\displaystyle \int\limits_{-\infty }^{\infty }\frac{ dx}{x^{2}+4x+5}$	$\displaystyle =\lim_{a\rightarrow -\infty }\int\limits_{a}^{0}\frac{ dx}{x^{2}+4x+5}+\lim_{b\rightarrow \infty }\int\limits_{0}^{b}\frac{ dx}{x^{2}+4x+5}$
	$\displaystyle =\lim_{a\rightarrow -\infty }\int\limits_{a}^{0}\frac{ dx}{\left... ...{b\rightarrow \infty }\int\limits_{0}^{b}\frac{ dx}{ \left( x+2\right) ^{2}+1}$
	$\displaystyle =\lim_{a\rightarrow -\infty }\mathop{\mathrm{arctg}}\nolimits \le... ...w \infty }\mathop{\mathrm{arctg}}\nolimits \left( x+2\right) \bigg\vert_{0}^{b}$
	$\displaystyle =\lim_{a\rightarrow -\infty }\left[ \mathop{\mathrm{arctg}}\nolim... ...m{arctg}}\nolimits \left( b+2\right) -\mathop{\mathrm{arctg}}\nolimits 2\right]$
	$\displaystyle =\mathop{\mathrm{arctg}}\nolimits 2+\frac{\pi }{2}+\frac{\pi }{2}- \mathop{\mathrm{arctg}}\nolimits 2=\pi .$

c)

Vrijedi

$\displaystyle \int\limits_{-1}^{1}\frac{ dx}{x^{3}}$	$\displaystyle =\int\limits_{-1}^{0}\frac{ dx}{x^{3}} +\int\limits_{0}^{1}\frac... ...+\lim_{\delta \rightarrow \infty }\int\limits_{0+\delta }^{1}\frac{ dx}{x^{3}}$
	$\displaystyle =\lim_{\varepsilon \rightarrow 0}\frac{-1}{2x^{2}}\bigg\vert _{-1... ...}+\lim_{\delta \rightarrow \infty }\frac{-1}{2x^{2}} \bigg\vert_{0+\delta }^{1}$
	$\displaystyle =\lim_{\varepsilon \rightarrow 0}\left( \frac{-1}{2\varepsilon ^{... ...m_{\delta \rightarrow 0}\left( \frac{-1}{2}+\frac{1}{ 2\varepsilon ^{2}}\right)$
	$\displaystyle =\frac{1}{2}\lim_{\delta \rightarrow 0}\frac{1}{\delta ^{2}}-\frac{1}{2} \lim_{\varepsilon \rightarrow 0}\frac{1}{\varepsilon ^{2}}=\infty -\infty,$

pa integral divergira.

Supstitucija i parcijalna integracija ODREĐENI INTEGRAL Površina ravninskog lika
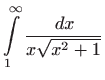
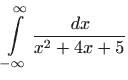
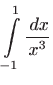
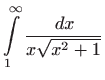
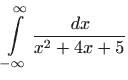
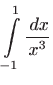