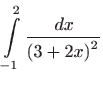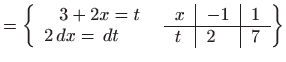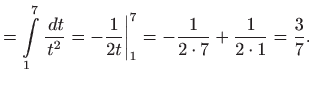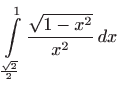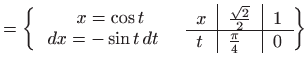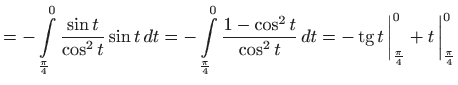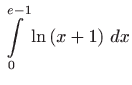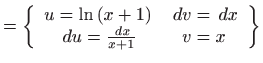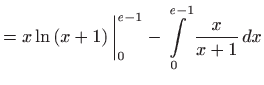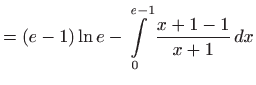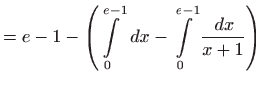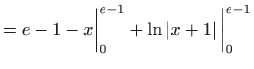☰ matematika2

Newton-Leibnitzova formula ODREĐENI INTEGRAL Nepravi integral

Supstitucija i parcijalna integracija

Izračunajte integrale:

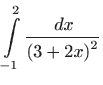a): $\displaystyle\int\limits_{-1}^{2}\frac{ dx}{\left( 3+2x\right) ^{2} }$ ,
b)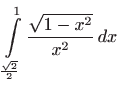: $\displaystyle\int\limits_{\frac{\sqrt{2}}{2}}^{1}\frac{\sqrt{ 1-x^{2}}}{x^{2}} dx$ ,
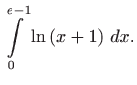c): $\displaystyle\int\limits_{0}^{e-1}\ln \left( x+1\right) dx.$ .

Rješenje.

a)

Vrijedi

$\displaystyle \int\limits_{-1}^{2}\frac{ dx}{\left( 3+2x\right) ^{2}}$	$\displaystyle =\left\{ \begin{array}{c} 3+2x=t 2 dx= dt \quad \quad \end{a... ...\vert l} $x$ & $-1$ & $1$ \hline $t$ & $2$ & $7$ \end{tabular} \right\}$
	$\displaystyle =\int\limits_{1}^{7}\frac{ dt}{t^{2}}=-\frac{1}{2t}\bigg\vert _{1}^{7}=-\frac{1}{2\cdot 7}+\frac{1}{2\cdot 1}=\frac{3}{7}.$

b)

Iz formule parcijalne integracije

[*]

[M2, teorem 1.7] slijedi

$\displaystyle \int\limits_{\frac{\sqrt{2}}{2}}^{1}\frac{\sqrt{1-x^{2}}}{x^{2}} dx$	$\displaystyle =\left\{ \begin{array}{c} x=\cos t dx=-\sin t dt \quad \end... ...2}}{2}}$ & $1$ \hline $t$ & $\frac{\pi}{4}$ & $0$ \end{tabular} \right\}$
	$\displaystyle =-\int\limits_{\frac{\pi }{4}}^{0}\frac{\sin t}{\cos ^{2}t}\sin t... ...limits t \bigg\vert_{\frac{\pi }{4}}^{0}+t \bigg\vert_{\frac{\pi }{4}}^{0}$
	$\displaystyle =1-\frac{\pi }{4}.$

c)

Vrijedi

$\displaystyle \int\limits_{0}^{e-1}\ln \left( x+1\right) dx$	$\displaystyle =\left\{ \begin{array}{cc} u=\ln \left( x+1\right) & dv= dx du=\frac{ dx}{x+1} & v=x \end{array} \right\}$
	$\displaystyle =x\ln \left( x+1\right) \bigg\vert_{0}^{e-1}-\int\limits_{0}^{e-1}\frac{x}{ x+1} dx$
	$\displaystyle =\left( e-1\right) \ln e-\int\limits_{0}^{e-1}\frac{x+1-1}{x+1} dx$
	$\displaystyle =e-1-\left( \int\limits_{0}^{e-1} dx-\int\limits_{0}^{e-1}\frac{ dx}{x+1} \right)$
	$\displaystyle =e-1-x\bigg\vert_{0}^{e-1}+\ln \left\vert x+1\right\vert \bigg\vert _{0}^{e-1}$
	$\displaystyle =e-1-\left( e-1\right) +\ln e=1.$

Newton-Leibnitzova formula ODREĐENI INTEGRAL Nepravi integral
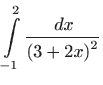
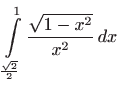
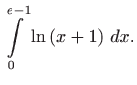
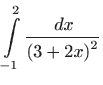
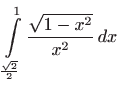
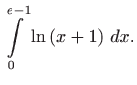