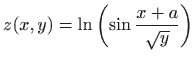Parcijalna derivacija prvog reda

Odredite parcijalne derivacije prvog reda za sljedeće funkcije:

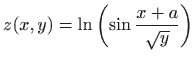a): $\displaystyle z(x,y)=\ln \left(\sin \frac{x+a}{\sqrt y}\right)$ ,
b): $\displaystyle u(x,y,z)=(xy)^z$ .

Rješenje.

Tražene derivacije odredit ćemo primjenom već poznatih pravila deriviranja [M1, poglavlje 5.1.3], ali na način da, kada funkciju $\displaystyle z(x,y)$ deriviramo po varijabli , tada varijablu tretiramo kao konstantu, i obrnuto:

a)

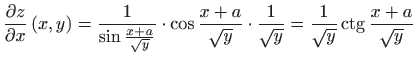$\displaystyle \frac{\partial z}{\partial x}\left( x,y\right)=\frac{1}{\sin \fr... ...}{\sqrt y} =\frac{1}{\sqrt y}\mathop{\mathrm{ctg}}\nolimits \frac{x+a}{\sqrt y}$ .

Analogno vrijedi:

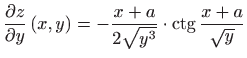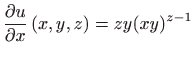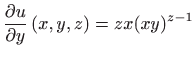$\displaystyle \frac{\partial z}{\partial y}\left( x,y\right)=-\frac{x+a}{2\sqrt {y^3}}\cdot \mathop{\mathrm{ctg}}\nolimits \frac{x+a}{\sqrt y}$ .

b)

$\displaystyle \frac{\partial u}{\partial x}\left( x,y,z\right)=zy(xy)^{z-1}$ ,

$\displaystyle \frac{\partial u}{\partial y}\left( x,y,z\right)=zx(xy)^{z-1}$ i

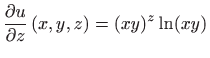$\displaystyle \frac{\partial u}{\partial z}\left( x,y,z\right)=(xy)^z\ln (xy)$ .