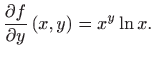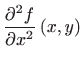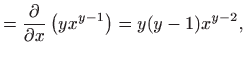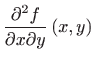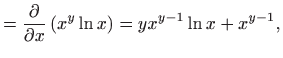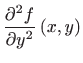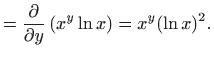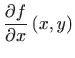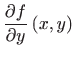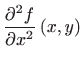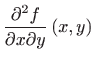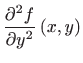☰
matematika2
Parcijalna derivacija prvog reda
FUNKCIJE VIŠE VARIJABLA
Parcijalna derivacija trećeg reda
Parcijalna derivacija drugog reda
Odredite parcijalne derivacije drugog reda za funkcije:
- a)
-
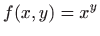 ,
,
- b)
-
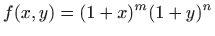 u točki
u točki 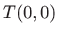 (
(
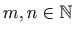 ).
).
Rješenje.
- a)
- Odredimo najprije parcijalne derivacije prvog reda zadane funkcije. Vrijedi
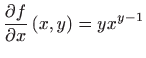 i i 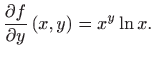 |
|
Sada je prema
![[*]](../icons.gif/crossref.gif) [M2, definicija 3.8]
[M2, definicija 3.8]
- b)
- Parcijalne derivacije prvog reda funkcije
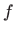 u proizvoljnoj točki
u proizvoljnoj točki
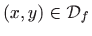 glase:
glase:
Parcijalne derivacije drugog reda funkcije 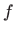 u proizvoljnoj točki
u proizvoljnoj točki
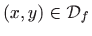 su:
su:
Prema tome, vrijednosti parcijalnih derivacija drugog reda funkcije 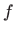 u točki
u točki 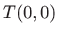 su:
su:
Parcijalna derivacija prvog reda
FUNKCIJE VIŠE VARIJABLA
Parcijalna derivacija trećeg reda
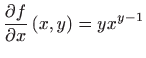 i
i